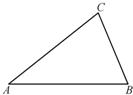
摘要：22．如下图.已知点D为△ABC的边.BC的延长线上的一点,DF⊥AB于点F.交AC于点E.且∠A=35°.∠D=42°.求∠ACD的度数?
网址：http://m.1010jiajiao.com/timu_id_737398[举报]
如下图，△ABC中，已知
BAC =45，AD⊥BC于点D，BD =2，DC =3，求AD的长。小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题。
请按照小萍的思路，探究并解答下列问题：
（1）分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，证明四边形AEGF是正方形；
（2）设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值。
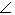BAC =45，AD⊥BC于点D，BD =2，DC =3，求AD的长。小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题。请按照小萍的思路，探究并解答下列问题：
（1）分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，证明四边形AEGF是正方形；
（2）设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值。
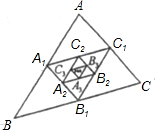如图，已知△ABC的周长为1，分别连接AB，BC，CA各边的中点得△A1B1C1，再连接A1B1，B1C1，C1A1的中点得△A2B2C2，…，这样延续下去，最后得△AnBnCn．那么△AnBnCn的周长等于
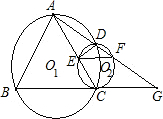如图，已知等边三角形△ABC内接于⊙O1，⊙O2与BC相切于C，与AC相交于E，与⊙O1相交于另一点D，直线AD交⊙O2于另一点F，交BC的延长线于G，点F为AG的中点．对于如下四个结论：①EF∥BC；②BC=FC；③DE•AG=AB•EC；④弧AD=弧DC．其中一定成立的是（ ）| A、①②④ | B、②③ | C、①③④ | D、①②③④ |
