摘要：如图.在平面直角坐标系中.直线y＝与x轴.y轴分别交于A.B两点.将△ABO绕原点O顺时针旋转得到△A´B´O.并使OA´⊥AB.垂足为D.直线AB与线段A´B´相交于点G．动点E从原点O出发.以1个单位/秒的速度沿x轴正方向运动.设动点E运动的时间为t秒．(1)求点D的坐标,(2)连接DE.当DE与线段OB´相交.交点为F.且四边形DFB´G是平行四边形时.求此时线段DE所在的直线的解析式,
网址：http://m.1010jiajiao.com/timu_id_733747[举报]
如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．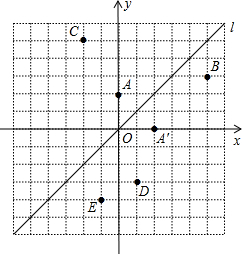
实验与探究：
（1）由图观察易知A（0，2）关于直线l的对称点A′（2，0）的坐标为（2，0），请在图中分别标明B（5，3）、C（-2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′ 、C′ ；
归纳与发现：
（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为 （不必证明）；
运用与拓广：
（3）已知两点D（1，-3）、E（-1，-4），试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标． 查看习题详情和答案>>
实验与探究：
（1）由图观察易知A（0，2）关于直线l的对称点A′（2，0）的坐标为（2，0），请在图中分别标明B（5，3）、C（-2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′
归纳与发现：
（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为
运用与拓广：
（3）已知两点D（1，-3）、E（-1，-4），试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标． 查看习题详情和答案>>
如图，在平面直角坐标系中，直线AB与Y轴和X轴分别交于点A、点B，与反比例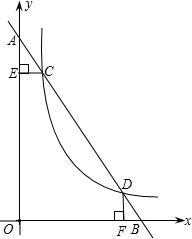
函数y=
在第一象限的图象交于点c（1，6）、点D（3，n）．过点C作CE上y轴于E，过点D作DF上x轴于F．
（1）求m，n的值；
（2）求直线AB的函数解析式；
（3）求证：△AEC≌△DFB． 查看习题详情和答案>>
函数y=| m | x |
（1）求m，n的值；
（2）求直线AB的函数解析式；
（3）求证：△AEC≌△DFB． 查看习题详情和答案>>
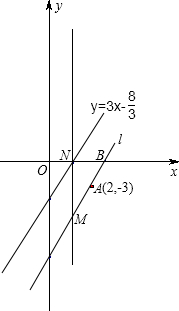如图，在平面直角坐标系中，直线l经过点A（2，-3），与x轴交于点B，且与直线y=3x-| 8 |
| 3 |
（1）求：直线l的函数解析式及点B的坐标；
（2）如直线l上有一点M（a，-6），过点M作x轴的垂线，交直线y=3x-
| 8 |
| 3 |
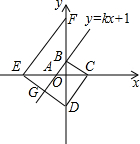如图，在平面直角坐标系中，直线y=kx+1分别交x轴，y轴于点A，B，过点B作BC⊥AB交x轴于点C，过点C作CD⊥BC交y轴于点D，过点D作DE⊥CD交轴于点x E，过点E作EF⊥DE交y轴于点F．已知点A恰好是线段EC的中点，那么线段EF的长是
如图，在平面直角坐标系中，直线y=