摘要:25.正方形ABCD的对角线交点为O.两条对角线把它分成了四个面积相等的三角形.(1)平行四边形ABCD的两条对角线交点为O.若△AOB.△BOC.△COD.△DOA面积分别为S1.S2.S3.S4.试判断S1.S2.S3.S4的关系.并加以证明,(2)四边形ABCD的两条对角线互相垂直.交点为O.若△AOB.△BOC.△COD.△DOA面积分别为S1.S2.S3.S4.试判断S1.S2.S3.S4的关系.并加以证明,(3)四边形ABCD的两条对角线交点为O.若△AOB.△BOC.△COD.△DOA面积分别为S1.S2.S3.S4.试判断S1.S2.S3.S4的关系.并加以证明,(4)四边形ABCD的两条对角线相等.交点为O.∠BAC=∠BDC,若△AOB.△BOC.△COD.△DOA面积分别为S1.S2.S3.S4.试只用S1.S3或只用S2.S4表示四边形ABCD的面积S.
网址:http://m.1010jiajiao.com/timu_id_731088[举报]
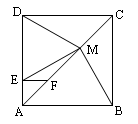

 :MB=MD;
:MB=MD;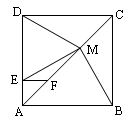
 :MB=MD;
:MB=MD;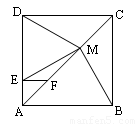
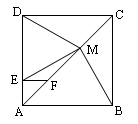
 :MB=MD;
:MB=MD;