摘要:思考:对于函数.当自变量取一对相反数时.函数值也得到一对相反数.则
网址:http://m.1010jiajiao.com/timu_id_725817[举报]
阅读下列材料再回答问题:
对于函数y=x2,当x=1时,y=1,当x=-1时,y=1;当x=2时,y=4,当x=-2时,y=4;…
而点(1,1)与(-1,1),(2,4)与(-2,4),…,都关于y轴对称.显然,如果点(x0,y0)在函数y=x2的图象上,那么,它关于y轴对称的点(-x0,y0)也在函数y=x2的图象上,这时,我们说函数y=x2关于y轴对称.
一般地,如果对于一个函数,当自变量x在允许范围内取值时,若x=x0和x=-x0时,函数值都相等,我们说函数的图象关于y轴对称.
问题:
(1)对于函数y=x3,当自变量x取一对相反数时,函数值也得到一对相反数,则函数y=x3的图象关于
(2)下列函数:①y=x3+2x;②y=2x4+4x2;③y=x+
;④y=-x-2 中,其图象关于y轴对称的有
(3)请你写出一个我们学过的函数关系式
查看习题详情和答案>>
对于函数y=x2,当x=1时,y=1,当x=-1时,y=1;当x=2时,y=4,当x=-2时,y=4;…
而点(1,1)与(-1,1),(2,4)与(-2,4),…,都关于y轴对称.显然,如果点(x0,y0)在函数y=x2的图象上,那么,它关于y轴对称的点(-x0,y0)也在函数y=x2的图象上,这时,我们说函数y=x2关于y轴对称.
一般地,如果对于一个函数,当自变量x在允许范围内取值时,若x=x0和x=-x0时,函数值都相等,我们说函数的图象关于y轴对称.
问题:
(1)对于函数y=x3,当自变量x取一对相反数时,函数值也得到一对相反数,则函数y=x3的图象关于
原点
原点
对称.(“x轴”、“y轴”或“原点”).(2)下列函数:①y=x3+2x;②y=2x4+4x2;③y=x+
| 1 |
| x |
②④
②④
,关于原点对称的有①③
①③
(只填序号).(3)请你写出一个我们学过的函数关系式
y=
(k≠0)
| k |
| x |
y=
(k≠0)
,其图象关于直线y=x对称.| k |
| x |
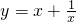 ;④y=-x-2 中,其图象关于y轴对称的有______,关于原点对称的有______(只填序号).
;④y=-x-2 中,其图象关于y轴对称的有______,关于原点对称的有______(只填序号). ,当自变量
,当自变量 取两个不同的值
取两个不同的值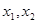 时函数值相等,则当自变量
时函数值相等,则当自变量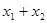 时函数值与(
)
时函数值与(
)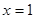 时的函数值相等 B.
时的函数值相等 B. 时的函数值相等
时的函数值相等 时的函数值相等 D.
时的函数值相等 D. 时的函数值相等
时的函数值相等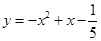 ,当自变量
,当自变量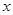 取
取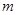 时,对应的函数值大于0,当自变量
时,对应的函数值大于0,当自变量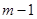 ,
,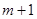 时对应的函数值
时对应的函数值 、
、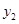 ,则
,则 ,当自变量
,当自变量 取
取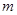 时,对应的函数值大于0,当自变量
时,对应的函数值大于0,当自变量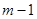 ,
, 时对应的函数值
时对应的函数值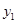 、
、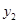 ,则
,则