摘要：+P(B)所以他可能是乘飞机来也可能是乘火车或汽车来的．--13分
网址：http://m.1010jiajiao.com/timu_id_72307[举报]
某企业准备投产一批特殊型号的产品，已知该种产品的成本C与产量q的函数关系式为C=
-3q2+20q+10(q＞0)．该种产品的市场前景无法确定，有三种可能出现的情况，各种情形发生的概率及产品价格p与产量q的函数关系式如下表所示：
设L1，L2，L3分别表示市场情形好、中差时的利润，随机变量ξq，表示当产量为q，而市场前景无法确定的利润．
（Ⅰ）分别求利润L1，L2，L3与产量q的函数关系式；
（Ⅱ）当产量q确定时，求期望Eξq，试问产量q取何值时，Eξq取得最大值． 查看习题详情和答案>>
| q3 |
| 3 |
| 市场情形 | 概率 | 价格p与产量q的函数关系式 |
| 好 | 0.4 | p=164-3q |
| 中 | 0.4 | p=101-3q |
| 差 | 0.2 | p=70-3q |
（Ⅰ）分别求利润L1，L2，L3与产量q的函数关系式；
（Ⅱ）当产量q确定时，求期望Eξq，试问产量q取何值时，Eξq取得最大值． 查看习题详情和答案>>
某种圆形射击靶由三个同心圆构成(如右图),从里到外的三个区域分别记为A、B、C，（B、C为圆环），某射手一次射击中，击中A、B、C区域的概率分别为P（A）=0.4,P(B)=0.25，P(C)=0.2，没有中靶的概率为P（D）.
（1）求P（D）；
（2）该射手一次射击中，求击中A区或B区的概率；
（3）该射手共射击三次，求恰有两次击中A区的概率.
查看习题详情和答案>>| 该种产品的市场前景无法确定，有三种可能出现的情况，各种情形发生的概率及产品价格p与产量q的函数关系式如下表所示： | ||||||||||||
| ||||||||||||
| （1）分别求利润L1，L2，L3与产量q的函数关系式； （2）当产量q确定时，求期望Eξk； （3）试问产量q取何值时，Eξk取得最大值。 |
某企业准备投产一批特殊型号的产品，已知该种产品的成本C与产量q的函数关系式为C=
-3q2+20q+10(q＞0)．该种产品的市场前景无法确定，有三种可能出现的情况，各种情形发生的概率及产品价格p与产量q的函数关系式如下表所示：
设L1，L2，L3分别表示市场情形好、中差时的利润，随机变量ξk，表示当产量为q，而市场前景无法确定的利润．
（I）分别求利润L1，L2，L3与产量q的函数关系式；
（II）当产量q确定时，求期望Eξk，试问产量q取何值时，Eξk取得最大值．
查看习题详情和答案>>
| q3 |
| 3 |
| 市场情形 | 概率 | 价格p与产量q的函数关系式 |
| 好 | 0.4 | p=164-3q |
| 中 | 0.4 | p=101-3q |
| 差 | 0.2 | p=70-3q |
（I）分别求利润L1，L2，L3与产量q的函数关系式；
（II）当产量q确定时，求期望Eξk，试问产量q取何值时，Eξk取得最大值．
现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择.为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏.
（Ⅰ）求这4个人中恰有2人去参加甲游戏的概率；
（Ⅱ）求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；
（Ⅲ）用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记
，求随机变量
的分布列与数学期望
.
【解析】依题意，这4个人中，每个人去参加甲游戏的概率为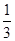
，去参加乙游戏的概率为
.
设“这4个人中恰有i人去参加甲游戏”为事件
则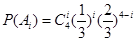
.
（1）这4个人中恰有2人去参加甲游戏的概率
（2）设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B，则
.由于
互斥，故
所以，这个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为
.
（3）的所有可能取值为0,2,4.由于
互斥，
互斥，故
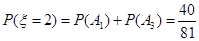
所以的分布列是
|
|
0 |
2 |
4 |
|
P |
|
|
|
随机变量的数学期望
.
查看习题详情和答案>>