题目内容
某企业准备投产一批特殊型号的产品，已知该种产品的成本C与产量q的函数关系式为C=
-3q2+20q+10(q＞0)．该种产品的市场前景无法确定，有三种可能出现的情况，各种情形发生的概率及产品价格p与产量q的函数关系式如下表所示：
设L1，L2，L3分别表示市场情形好、中差时的利润，随机变量ξk，表示当产量为q，而市场前景无法确定的利润．
（I）分别求利润L1，L2，L3与产量q的函数关系式；
（II）当产量q确定时，求期望Eξk，试问产量q取何值时，Eξk取得最大值．
| q3 |
| 3 |
| 市场情形 | 概率 | 价格p与产量q的函数关系式 |
| 好 | 0.4 | p=164-3q |
| 中 | 0.4 | p=101-3q |
| 差 | 0.2 | p=70-3q |
（I）分别求利润L1，L2，L3与产量q的函数关系式；
（II）当产量q确定时，求期望Eξk，试问产量q取何值时，Eξk取得最大值．
（I）根据所给的表格中的数据和题意写出
L1=(164-3q)•q-(
-3q2+20q+10)
=-
+144q-10(q＞0)．
同理可得L2=-
+81q-10(q＞0)．
L3=-
+50q-10(q＞0)．
（II）由期望定义可知Eξq=0.4L1+0.4L2+0.2L3
=0.4*(-
+144q-10)+0.4*(-
+81q-10)+0.28*(-
+50q-10)
=-
+100q-10．
可知Eξq是产量q的函数，设f(q)=Eξq=-
+100q-10(q＞0)，
得f'（q）=-q2+100．令f'（q）=0解得q=10，q=-10（舍去）．
由题意及问题的实际意义可知，当q=10时，f（q）取得最大值，即Eξq最大时的产量为10．
L1=(164-3q)•q-(
| q3 |
| 3 |
=-
| q3 |
| 3 |
同理可得L2=-
| q3 |
| 3 |
L3=-
| q3 |
| 3 |
（II）由期望定义可知Eξq=0.4L1+0.4L2+0.2L3
=0.4*(-
| q3 |
| 3 |
| q3 |
| 3 |
| q3 |
| 3 |
=-
| q3 |
| 3 |
可知Eξq是产量q的函数，设f(q)=Eξq=-
| q3 |
| 3 |
得f'（q）=-q2+100．令f'（q）=0解得q=10，q=-10（舍去）．
由题意及问题的实际意义可知，当q=10时，f（q）取得最大值，即Eξq最大时的产量为10．
练习册系列答案
相关题目
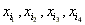(其中{i1，i2，i3，i4}={1，2，3，4})依次成等差数列？若存在，求所有的b及相应的x4；若不存在，说明理由． 
．
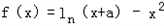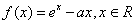有小于零的极值点，则实数a的取值范围为（ ）。