摘要:(1)证明:平面BAE⊥平面DAE,(2)求直线AE与平面DCE所成角的正弦值,(3)求二面角A―DE―C的余弦值.
网址:http://m.1010jiajiao.com/timu_id_70053[举报]
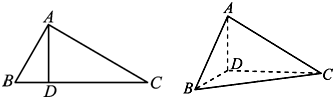 如图1-6,在△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,且BD=2,沿AD把△ABD折起,使∠BDC=90°.
如图1-6,在△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,且BD=2,沿AD把△ABD折起,使∠BDC=90°. (1)证明:平面ADB⊥平面BDC;
(2)求点D到平面ABC的距离.
 (2008•临沂二模)在三棱锥S-ABC中,△ABC是边长为4的正三角形,SB=2
(2008•临沂二模)在三棱锥S-ABC中,△ABC是边长为4的正三角形,SB=2| 5 |
| 3 |
(1)证明:平面SAC⊥平面ABC;
(2)求直线MN与平面SBC所成角的正弦值.
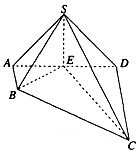 如图,在四棱锥S-ABCD,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=
如图,在四棱锥S-ABCD,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=| 3 |
(1)证明:平面SBE⊥平面SEC
(2)若SE=1,求直线CE与平面SBC所成角的余弦值.

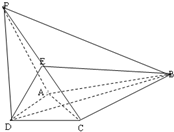 在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2
在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2