题目内容
如图,在△ABC中,∠ABC=60°,∠BAC=90°,AD是BC上的高,沿AD把△ABC折起,使∠BDC=60°.
(1)证明:平面ADB⊥平面BDC;
(2)设E为BC的中点,求异面直线AE与DB所成角的大小.
(1)证明:平面ADB⊥平面BDC;
(2)设E为BC的中点,求异面直线AE与DB所成角的大小.

分析:(1)已知在△ABC中,AD是BC上的高,沿AD把△ABC折起,使∠BDC=60°,可得AD⊥DC,AD⊥DB,根据面面垂直的判定定理进行求解;
(2)作辅助线,取DC中点F,连接EF,则EF∥BD,可得∠AEF为异面直线AE与BD所成的角,再根据余弦定理和向量公式进行求解;
(2)作辅助线,取DC中点F,连接EF,则EF∥BD,可得∠AEF为异面直线AE与BD所成的角,再根据余弦定理和向量公式进行求解;
解答: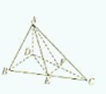 解:(1)∵折起前AD是BC边上的高,
解:(1)∵折起前AD是BC边上的高,
∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,∴AD⊥平面BDC,
∵AD?平面ABD,
∴平面ADB⊥平面BDC;
(2)取DC中点F,连接EF,则EF∥BD,
∴∠AEF为异面直线AE与BD所成的角(或其补角),
连接AF,DE,设BD=2,则EF=1,AD=2
,DC=6,DF=3,
在△BDC中,BC2=BD2+DC2-2BD•DCcos∠BDC=28,
cos∠DBC=
=-
,BE=
BC=
,
在△BDE中,DE2=BD2+BE2-2BDBEcos∠DBC=13,
在Rt△ADE中,AE=
=5,
在Rt△ADF中,AF=
=
,
在△AEF中,cos∠AEF=
=
,
所以异面直线AE与DB所成角为60°;
 解:(1)∵折起前AD是BC边上的高,
解:(1)∵折起前AD是BC边上的高,∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,∴AD⊥平面BDC,
∵AD?平面ABD,
∴平面ADB⊥平面BDC;
(2)取DC中点F,连接EF,则EF∥BD,
∴∠AEF为异面直线AE与BD所成的角(或其补角),
连接AF,DE,设BD=2,则EF=1,AD=2
| 3 |
在△BDC中,BC2=BD2+DC2-2BD•DCcos∠BDC=28,
cos∠DBC=
| BD2+BC2-DC2 |
| 2BD•BC |
| 1 | ||
2
|
| 1 |
| 2 |
| 7 |
在△BDE中,DE2=BD2+BE2-2BDBEcos∠DBC=13,
在Rt△ADE中,AE=
| AD2+DE2 |
在Rt△ADF中,AF=
| AD2+DF2 |
| 21 |
在△AEF中,cos∠AEF=
| AE2+EF2-AF2 |
| 2AE•EF |
| 1 |
| 2 |
所以异面直线AE与DB所成角为60°;
点评:此题主要考查面面垂直和异面直线夹角公式的求法,第二问解题的关键是作出辅助线,此题是一道中档题,也是高考必考题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知