摘要：24．如图.已知点E在△ABC的边AB上.点D在CA的延长线上.点F在BC的延长线上.问:∠ACF与∠D有何关系?并说明理由.
网址：http://m.1010jiajiao.com/timu_id_691059[举报]
如图，已知D是△ABC的边AB上一点，DF交AC于点E，DE=EF，FC∥AB，试说明AB-FC=BD．小明同学的思考过程如下，你能理解他的想法吗？试着在括号内写出理由．
证明：∵FC∥AB
∴∠A=∠ECF （
在△ADE和△CFE中
∵DE=EF
∠A=∠ECF（已证）
∠AED=∠CEF （
∴△ADE≌△CFE （
∴AD=FC （
又∵AB-AD=BD
∴AB-FC=BD．
查看习题详情和答案>>
证明：∵FC∥AB
∴∠A=∠ECF （
两直线平行，内错角相等
两直线平行，内错角相等
）在△ADE和△CFE中
∵DE=EF
∠A=∠ECF（已证）
∠AED=∠CEF （
对顶角相等
对顶角相等
）∴△ADE≌△CFE （
AAS
AAS
）∴AD=FC （
全等三角形的对应边相等
全等三角形的对应边相等
）又∵AB-AD=BD
∴AB-FC=BD．
如图，已知D是△ABC的边AB上一点，DF交AC于点E，DE=EF，FC∥AB，试说明AB-FC=BD．小明同学的思考过程如下，你能理解他的想法吗？试着在括号内写出理由．
证明：∵FC∥AB
∴∠A=∠ECF （________）
在△ADE和△CFE中
∵DE=EF
∠A=∠ECF（已证）
∠AED=∠CEF （________）
∴△ADE≌△CFE （________）
∴AD=FC （________）
又∵AB-AD=BD
∴AB-FC=BD．
查看习题详情和答案>>
20、如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．（1）求证：AE=DF；
（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
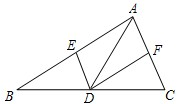22、如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．
9、如图，已知点P是不等边△ABC的边BC上的一点，点D在边AB或AC上，若由点P、D截得的小三角形与△ABC相似，那么D点的位置最多有（ ）