题目内容
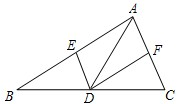 22、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
22、如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.(1)求证:AE=DF;
(2)若添加条件
∠BAC=90°
,则四边形AEDF是矩形;若添加条件
AB=AC
,则四边形AEDF是菱形;若添加条件
△ABC是等腰直角三角形
,则四边形AEDF是正方形.分析:(1)由题意易得四边形AEDF是平行四边形,∴AE=DF;
(2)因为有一直角的平行四边形形是矩形,可添加条件:∠BAC=90°;邻边相等的平行四边形是菱形,可添加条件:AB=AC;正方形的邻边相等且四个角都为直角,可添加条件:△ABC是等腰直角三角形.
(2)因为有一直角的平行四边形形是矩形,可添加条件:∠BAC=90°;邻边相等的平行四边形是菱形,可添加条件:AB=AC;正方形的邻边相等且四个角都为直角,可添加条件:△ABC是等腰直角三角形.
解答:(1)证明:∵DE∥ACDF∥AB,
∴四边形AEDF是平行四边形.
∴AE=DF.(4分)
(2)解:答案不唯一,只要正确就给分,每空(1分)如:∠BAC=90°,AB=AC,△ABC是等腰直角三角形(7分)
∴四边形AEDF是平行四边形.
∴AE=DF.(4分)
(2)解:答案不唯一,只要正确就给分,每空(1分)如:∠BAC=90°,AB=AC,△ABC是等腰直角三角形(7分)
点评:本题是开放题,可以针对各种特殊的平行四边形的判定方法,给出条件,再证明结论.答案可以有多种,主要条件明确,说法有理即可.

练习册系列答案
相关题目

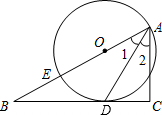 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证:
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证: 如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.
如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC. 如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=
如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=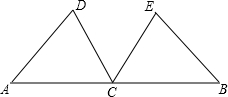 如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.
如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.