摘要:25.在平面直角坐标系.已知直线交于点C.交轴于点A.等腰直角三角板OBD的顶点D与点G重合.如图l6一①所示.把三角板绕着点O顺时针旋转.旋转角度为().使B点恰好落在AC上的.如图l6一②所示.
网址:http://m.1010jiajiao.com/timu_id_687842[举报]
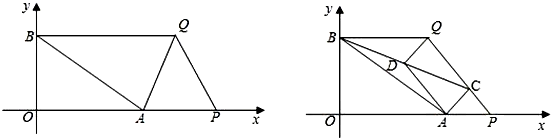
在平面直角坐标系中,已知点A(4,0),点B(0,3).点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q两点同时出发.
(1)连接AQ,当△ABQ是直角三角形时,求点Q的坐标;
(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;
(3)过点A作AC⊥AB,AC交射线PQ于点C,连接BC,D是BC的中点.在点P、Q的运动过程中,是否存在某时刻,使得以A、C、Q、D为顶点的四边形是平行四边形?若存在,试求出这时cot∠ABC的值;若不存在,试说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)连接AQ,当△ABQ是直角三角形时,求点Q的坐标;
(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;
(3)过点A作AC⊥AB,AC交射线PQ于点C,连接BC,D是BC的中点.在点P、Q的运动过程中,是否存在某时刻,使得以A、C、Q、D为顶点的四边形是平行四边形?若存在,试求出这时cot∠ABC的值;若不存在,试说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,
),直线l2的函数表达式为y=-
x+
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
(1)填空:直线l1的函数表达式是 ,交点P的坐标是 ,∠FPB的度数是 °;
(2)当⊙C和直线l2相切时,请证明点P到直线的距离CM等于⊙C的半径R,并写出R=3
-2时a的值;
(3)当⊙C和直线l2不相离时,已知⊙C的半径R=3
-2,记四边形NMOB的面积为S(其中点N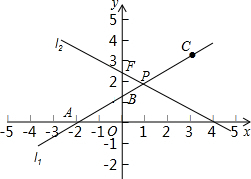 是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看习题详情和答案>>
是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看习题详情和答案>>
2
| ||
| 3 |
| ||
| 3 |
4
| ||
| 3 |
(1)填空:直线l1的函数表达式是
(2)当⊙C和直线l2相切时,请证明点P到直线的距离CM等于⊙C的半径R,并写出R=3
| 2 |
(3)当⊙C和直线l2不相离时,已知⊙C的半径R=3
| 2 |
 是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看习题详情和答案>>
是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看习题详情和答案>>
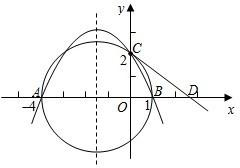 轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.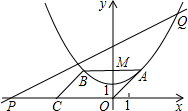 在平面直角坐标系xOy中,抛物线的解析式是y=
在平面直角坐标系xOy中,抛物线的解析式是y=