摘要：6．梯形总可以看成是一个平行四边形与一个三角形的组合.这也是我们解决有关梯形的问题时经常使用的方法.如图.梯形ABCD中.AD∥BC.DE∥AB.∠B=70°.∠C=40°.试说明:
网址：http://m.1010jiajiao.com/timu_id_686580[举报]
4、如图，是一个野营的帐篷，它可以看成是一个
中国，是拥有五千年历史的古国，它具有十分丰富的文化传承，其中京剧就是一门重要的艺术，常常受到外国友人的青睐．看到下面的京剧脸谱了吗？其实它们可以看成是一个半圆与抛物线的一部分组合成的封闭图形，如果一条直线与此图形只有一个交点，那么这条直线叫做它的切线．
如图，点A、B、C、D分别是该图形与坐标轴的交点，已知点D的坐标为（0，-3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．
（1）请你求出此图形抛物线部分的解析式，并写出自变量的取值范围；
（2）x轴上有点E（-3，0），直线CE是此图形的切线吗？请说明理由．
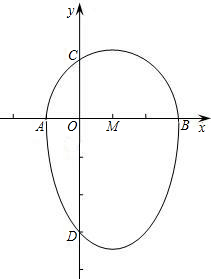
查看习题详情和答案>>
如图，点A、B、C、D分别是该图形与坐标轴的交点，已知点D的坐标为（0，-3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．
（1）请你求出此图形抛物线部分的解析式，并写出自变量的取值范围；
（2）x轴上有点E（-3，0），直线CE是此图形的切线吗？请说明理由．
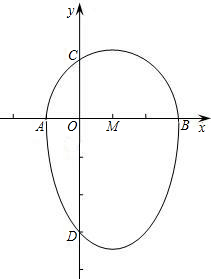
查看习题详情和答案>>
“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．例：在△ABC中，AB、BC、AC三边长分别是
| 5 |
| 10 |
| 13 |
小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：S△ABC=3×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
思维拓展：已知△ABC的边长分别为
| 5a |
| 2a |
| 17a |
“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
例：在△ABC中，AB、BC、AC三边长分别是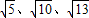
，求这个三角形的面积．
小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：
思维拓展：已知△ABC的边长分别为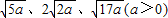
，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
查看习题详情和答案>>
例：在△ABC中，AB、BC、AC三边长分别是
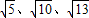，求这个三角形的面积．小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：
思维拓展：已知△ABC的边长分别为
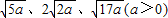，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
查看习题详情和答案>>
“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
例：在△ABC中，AB、BC、AC三边长分别是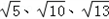
，求这个三角形的面积．小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即三角形的顶点都在小正方形的顶点处），
如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：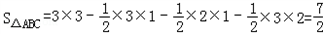
思维拓展：已知△ABC的边长分别为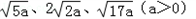
，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
例：在△ABC中，AB、BC、AC三边长分别是
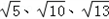，求这个三角形的面积．小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即三角形的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：
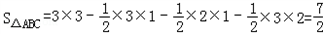
思维拓展：已知△ABC的边长分别为
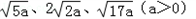，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．