题目内容
中国,是拥有五千年历史的古国,它具有十分丰富的文化传承,其中京剧就是一门重要的艺术,常常受到外国友人的青睐.看到下面的京剧脸谱了吗?其实它们可以看成是一个半圆与抛物线的一部分组合成的封闭图形,如果一条直线与此图形只有一个交点,那么这条直线叫做它的切线.如图,点A、B、C、D分别是该图形与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
(1)请你求出此图形抛物线部分的解析式,并写出自变量的取值范围;
(2)x轴上有点E(-3,0),直线CE是此图形的切线吗?请说明理由.
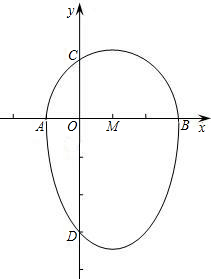

分析:(1)根据已知圆的圆心和半径求出A、B的坐标,再根据D点坐标求出抛物线解析式;
(2)求出CE解析式,并计算出M到直线CE的距离,与半径进行比较.
(2)求出CE解析式,并计算出M到直线CE的距离,与半径进行比较.
解答:解:(1)由圆M可知A(-1,0)B(3,0)且抛物线的对称轴为x=1
设抛物线的解析式为y=k(x-1)2+b(k≠0),
分别将A(-1,0)D(0,-3)代入
得二元一次方程组
解得:
所以抛物线的解析式为:y=(x-1)2-4(-1≤x≤3);
(2)由圆M得,C(0,
),
由E(-3,0)的直线CE的解析式为y=-
x-3
则M到直线CE的距离为
≠2,所以直线与圆不相切.
设抛物线的解析式为y=k(x-1)2+b(k≠0),
分别将A(-1,0)D(0,-3)代入
得二元一次方程组
|
解得:
|
所以抛物线的解析式为:y=(x-1)2-4(-1≤x≤3);
(2)由圆M得,C(0,
| 3 |
由E(-3,0)的直线CE的解析式为y=-
| ||
| 3 |
则M到直线CE的距离为
|-
| ||||||
|
点评:本题考查了抛物线解析式的求法以及切线的判定.

练习册系列答案
相关题目
 假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话:
假期测量超然楼的高度,在大明湖边一块平地上,甲和乙两名同学利用所带工具测量了一些数据,下面是他们的一段对话: 中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”.
中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”. 中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”.
中国拥有五千年悠久的历史,也出现了许多杰出的人物.例如,中国古代数学家-----宋朝赵爽用弦图(如图1)验证了一条几何学重要的定理:直角三角形两直角边的平方和等于斜边的平方,即a2+b2=c2.这就是著名的“勾股定理”.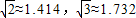 )
)