��Ŀ����
�����취����һ����Ҫ��������û�й̶���ģʽ��Ҫ���ú�������Ҫ������Ĺ۲졢�ḻ���������Ĺ�˼��Ӧ�ù��취����Ĺؼ��ж���һ��Ҫ����ȷ�ķ���ΪʲôĿ�Ķ����죻����ҪŪ�������ı����ص㣬�Ա����½�����ϣ�
�����ڡ�ABC�У�AB��BC��AC���߳��ֱ���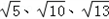 ������������ε������С���ڽ������ʱ����һ������������ÿ�������εı߳�Ϊ1�������������л�����㣨�������εĶ��㶼��С�����εĶ��㴦����
������������ε������С���ڽ������ʱ����һ������������ÿ�������εı߳�Ϊ1�������������л�����㣨�������εĶ��㶼��С�����εĶ��㴦����
��ͼ1��ʾ����������Ҫ��ĸߣ�����������ܼ�������������ͼ�е���������Կ�����һ���������ε������ȥ����С�����ε������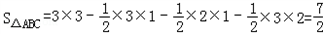
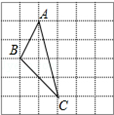
˼ά��չ����֪��ABC�ı߳��ֱ�Ϊ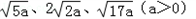 ��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������
��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������
�����ڡ�ABC�У�AB��BC��AC���߳��ֱ���
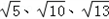 ������������ε������С���ڽ������ʱ����һ������������ÿ�������εı߳�Ϊ1�������������л�����㣨�������εĶ��㶼��С�����εĶ��㴦����
������������ε������С���ڽ������ʱ����һ������������ÿ�������εı߳�Ϊ1�������������л�����㣨�������εĶ��㶼��С�����εĶ��㴦������ͼ1��ʾ����������Ҫ��ĸߣ�����������ܼ�������������ͼ�е���������Կ�����һ���������ε������ȥ����С�����ε������
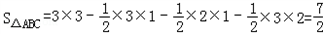
˼ά��չ����֪��ABC�ı߳��ֱ�Ϊ
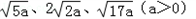 ��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������
��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������
�⣺��ͼ��AB=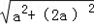 =
= ��
��
BC=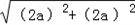 =
= ��
��
AC=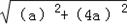 =
= ��
��
S��ABC=4a��2a�� ��a��2a��
��a��2a�� ��2a��2a��
��2a��2a�� ��a��4a=3a2��
��a��4a=3a2��
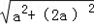 =
= ��
��BC=
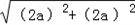 =
= ��
��AC=
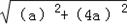 =
= ��
�� S��ABC=4a��2a��
 ��a��2a��
��a��2a�� ��2a��2a��
��2a��2a�� ��a��4a=3a2��
��a��4a=3a2��


��ϰ��ϵ�д�
 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�
�����Ŀ
 �����취����һ����Ҫ��������û�й̶���ģʽ��Ҫ���ú�������Ҫ������Ĺ۲졢�ḻ���������Ĺ�˼��Ӧ�ù��취����Ĺؼ��ж���һ��Ҫ����ȷ�ķ���ΪʲôĿ�Ķ����죻����ҪŪ�������ı����ص㣬�Ա����½�����ϣ�
�����취����һ����Ҫ��������û�й̶���ģʽ��Ҫ���ú�������Ҫ������Ĺ۲졢�ḻ���������Ĺ�˼��Ӧ�ù��취����Ĺؼ��ж���һ��Ҫ����ȷ�ķ���ΪʲôĿ�Ķ����죻����ҪŪ�������ı����ص㣬�Ա����½�����ϣ�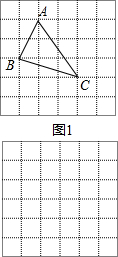 �����취����һ����Ҫ��������û�й̶���ģʽ��Ҫ���ú�������Ҫ������Ĺ۲졢�ḻ���������Ĺ�˼��Ӧ�ù��취����Ĺؼ��ж���һ��Ҫ����ȷ�ķ���ΪʲôĿ�Ķ����죻����ҪŪ�������ı����ص㣬�Ա����½�����ϣ�
�����취����һ����Ҫ��������û�й̶���ģʽ��Ҫ���ú�������Ҫ������Ĺ۲졢�ḻ���������Ĺ�˼��Ӧ�ù��취����Ĺؼ��ж���һ��Ҫ����ȷ�ķ���ΪʲôĿ�Ķ����죻����ҪŪ�������ı����ص㣬�Ա����½�����ϣ�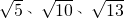 ������������ε������
������������ε������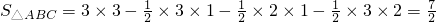
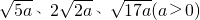 ��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������
��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������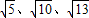 ������������ε������
�����������������
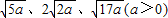 ��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������
��������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC����������������