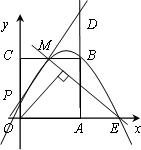摘要：(3)如图②.E为BC延长线上一动点.过A.B.E三点作⊙O’.连结AE.在⊙O’上另有一点F.且AF＝AE.AF交BC于点G.连结BF.下列结论:①BE+BF的值不变,②.其中有且只有一个成立.请你判断哪一个结论成立.并证明成立的结论.
网址：http://m.1010jiajiao.com/timu_id_686152[举报]
如图，已知在边长为1的正方形ABCD中，以D为圆心、DA为半径画弧
，E是AB上的一动点，过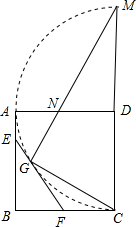
E作
的切线交BC于点F，切点为G，连GC，过G作GC的垂线交AD与N，交CD的延长线于M．
（1）求证：AE=EG，GF=FC；
（2）设AE=x，用含x的代数式表示FC的长；
（3）在图中，除GF以外，是否还存在与FC相等的线段，是哪些？试证明或说明理由；
（4）当△GDN是等腰三角形时，求AE的长． 查看习题详情和答案>>
 |
| AC |
E作 |
| AC |
（1）求证：AE=EG，GF=FC；
（2）设AE=x，用含x的代数式表示FC的长；
（3）在图中，除GF以外，是否还存在与FC相等的线段，是哪些？试证明或说明理由；
（4）当△GDN是等腰三角形时，求AE的长． 查看习题详情和答案>>
如图，已知在边长为1的正方形ABCD中，以D为圆心、DA为半径画弧
，E是AB上的一动点，过
E作
的切线交BC于点F，切点为G，连GC，过G作GC的垂线交AD与N，交CD的延长线于M．
（1）求证：AE=EG，GF=FC；
（2）设AE=x，用含x的代数式表示FC的长；
（3）在图中，除GF以外，是否还存在与FC相等的线段，是哪些？试证明或说明理由；
（4）当△GDN是等腰三角形时，求AE的长．
查看习题详情和答案>>
 |
| AC |
E作 |
| AC |
（1）求证：AE=EG，GF=FC；
（2）设AE=x，用含x的代数式表示FC的长；
（3）在图中，除GF以外，是否还存在与FC相等的线段，是哪些？试证明或说明理由；
（4）当△GDN是等腰三角形时，求AE的长．
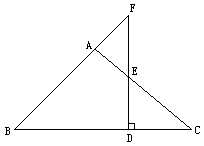
如图，△ABC中，AB=AC，E是线段AC上异于A、C的一个动点，过E作ED⊥BC于D，交直线BA于F．
①当E移动时，试判别△AEF是否为等腰三角形，并证明你的结论．
②当E在CA的延长线上，其余条件不变，①的结论是否仍成立?画出图形，并说明理由．
查看习题详情和答案>>
如图，在平面直角坐标系xOy中，△ABC三个机战的坐标分别为A(－6，0)，B(6，0)，C(0，4
)，延长AC到点D，使CD＝
AC，过点D作DE∥AB交BC的延长线于点E．
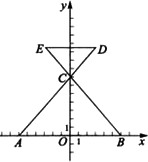
(1)求D点的坐标；
(2)作C点关于直线DE的对称点F，分别连结DF、EF，若过B点的直线y＝kx＋b将四边形CDFE分成周长相等的两个四边形，确定此直线的解析式；
(3)设G为y轴上一点，点P从直线y＝kx＋b与y轴的交点出发，先沿y轴到达G点，再沿GA到达A点，若P点在y轴上运动的速度是它在直线GA上运动速度的2倍，试确定G点的位置，使P点按照上述要求到达A点所用的时间最短．(要求：简述确定G点位置的方法，但不要求证明)
