题目内容
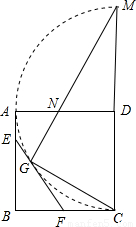
如图,已知在边长为1的正方形ABCD中,以D为圆心、DA为半径画弧 |
| AC |
 E作
E作 |
| AC |
(1)求证:AE=EG,GF=FC;
(2)设AE=x,用含x的代数式表示FC的长;
(3)在图中,除GF以外,是否还存在与FC相等的线段,是哪些?试证明或说明理由;
(4)当△GDN是等腰三角形时,求AE的长.
分析:(1)根据切线长定理即可得出AE=EG,GF=FC.
(2)根据(1)的结果,那么EF=AE+FC,我们用AE表示出BE,用CF表示出BF,那么可用勾股定理在三角形EBF中求出AE和CF的关系.
(3)应该是ND,可通过构建全等三角形来求解,连接DF,关键是证三角形MND和DFC全等.根据切线长定理和垂径定理,那么DF⊥CG,由于BC是切线,因此∠FCG=∠GMC,根据同角的余角相等可得出∠FDC=∠FCG=∠GMC,又有一组直角,DM=DC(都是半径)由此可得出两三角形全等,那么ND=FC.
(4)如果GDN是等腰三角形,那么只有一种情况GN=ND,此时三角形GND和CGF全等,此时DG=GC=DC,因此可得出三角形DGC是等边三角形,(2)中得出了用x表示CF的式子,那么可在直角三角形MDN中根据特殊角30°和MD即正方形的边长来得出DN的值,然后求出x即可得出AE的长.
(2)根据(1)的结果,那么EF=AE+FC,我们用AE表示出BE,用CF表示出BF,那么可用勾股定理在三角形EBF中求出AE和CF的关系.
(3)应该是ND,可通过构建全等三角形来求解,连接DF,关键是证三角形MND和DFC全等.根据切线长定理和垂径定理,那么DF⊥CG,由于BC是切线,因此∠FCG=∠GMC,根据同角的余角相等可得出∠FDC=∠FCG=∠GMC,又有一组直角,DM=DC(都是半径)由此可得出两三角形全等,那么ND=FC.
(4)如果GDN是等腰三角形,那么只有一种情况GN=ND,此时三角形GND和CGF全等,此时DG=GC=DC,因此可得出三角形DGC是等边三角形,(2)中得出了用x表示CF的式子,那么可在直角三角形MDN中根据特殊角30°和MD即正方形的边长来得出DN的值,然后求出x即可得出AE的长.
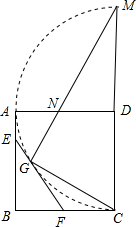
解答: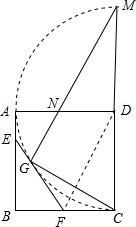 解:(1)由于EA、EF、FC都是圆D的切线,且A、G、C是切点,
解:(1)由于EA、EF、FC都是圆D的切线,且A、G、C是切点,
因此根据切线长定理,可得出AE=EG,GF=FC;
(2)设FC=t,BE=1-x,BF=1-t,EF=x+t,
在直角三角形BEF中,(1-x)2+(1-t)2=(x+t)2,
解出t=
,
∴FC=
;
(3)存在,ND=FC,GF是⊙D的切线,
∴∠DGF=90°,
连DF,那么DF平分弧GC,且DF⊥CG,
∵∠FCG=90°-∠GCD,∠GMC=90°-∠GCD,
∴∠FCG=∠GMC,
∵∠MDN=∠DCF=90°,MD=DC,
∴△MDN≌△DCF,
∴DN=FC;
(4)当△GDN是等腰三角形时,只能有GN=ND,
∴△GDN≌△GFC,
∴GD=DC=CG,∠DGC=60°,ND=MDtan30°=
=
,
∴x=2-
.
 解:(1)由于EA、EF、FC都是圆D的切线,且A、G、C是切点,
解:(1)由于EA、EF、FC都是圆D的切线,且A、G、C是切点,因此根据切线长定理,可得出AE=EG,GF=FC;
(2)设FC=t,BE=1-x,BF=1-t,EF=x+t,
在直角三角形BEF中,(1-x)2+(1-t)2=(x+t)2,
解出t=
| 1-x |
| 1+x |
∴FC=
| 1-x |
| 1+x |
(3)存在,ND=FC,GF是⊙D的切线,
∴∠DGF=90°,
连DF,那么DF平分弧GC,且DF⊥CG,
∵∠FCG=90°-∠GCD,∠GMC=90°-∠GCD,
∴∠FCG=∠GMC,
∵∠MDN=∠DCF=90°,MD=DC,
∴△MDN≌△DCF,
∴DN=FC;
(4)当△GDN是等腰三角形时,只能有GN=ND,
∴△GDN≌△GFC,
∴GD=DC=CG,∠DGC=60°,ND=MDtan30°=
| ||
| 3 |
| 1-x |
| 1+x |
∴x=2-
| 3 |
点评:本题主要考查了切线长定理、垂径定理,正方形的性质和全等三角形的判定等知识点.根据切线的性质得出角的度数或边相等是解题的关键.

练习册系列答案
相关题目
 如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长.
如图,已知:边长为1的正方形ABCD顶点都在⊙O上,P为边CD的中点,直线AP交圆于E点.求弦DE的长. ,E是AB上的一动点,过
,E是AB上的一动点,过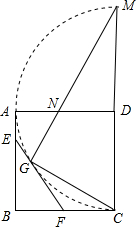 E作
E作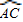 ,E是AB上的一动点,过E作
,E是AB上的一动点,过E作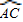 的切线交BC于点F,切点为G,连GC,过G作GC的垂线交AD与N,交CD的延长线于M.
的切线交BC于点F,切点为G,连GC,过G作GC的垂线交AD与N,交CD的延长线于M.