摘要：(3)如果取的中点.以为边在内部作如图2所示的矩形.点在线段上．设等边和矩形重叠部分的面积为.请求出当秒时与的函数关系式.并求出的最大值．

网址：http://m.1010jiajiao.com/timu_id_686092[举报]

如图，在直角坐标系中，O为坐标原点，矩形ABCD的边AD与x轴的正半轴重合，另三边都在第四象限内，已知点A（1，0），AB=2，AD=3，点E为OD的中点，以AD为直径作⊙M，经过A、D两点的抛物线y=ax²+bx+c的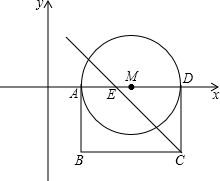

顶点为P．
（1）求经过C、E两点的直线的解析式；
（2）如果点P同时在⊙M和矩形ABCD内部，求a的取值范围；
（3）过点B作⊙M的切线交边CD于F点，当PF∥AD时，判断直线CE与y轴的交点是否在抛物线上，并说明理由．查看习题详情和答案>>

如图，在直角坐标系中，O为坐标原点，矩形ABCD的边AD与x轴的正半轴重合，另三边都在第四象限内，已知点A（1，0），AB=2，AD=3，点E为OD的中点，以AD为直径作⊙M，经过A、D两点的抛物线y=ax²+bx+c的顶点为P．
（1）求经过C、E两点的直线的解析式；
（2）如果点P同时在⊙M和矩形ABCD内部，求a的取值范围；
（3）过点B作⊙M的切线交边CD于F点，当PF∥AD时，判断直线CE与y轴的交点是否在抛物线上，并说明理由．

查看习题详情和答案>>

如图，在直角坐标系中，O为坐标原点，矩形ABCD的边AD与x轴的正半轴重合，另三边都在第四象限内，已知点A（1，0），AB=2，AD=3，点E为OD的中点，以AD为直径作⊙M，经过A、D两点的抛物线y=ax²+bx+c的顶点为P．
（1）求经过C、E两点的直线的解析式；
（2）如果点P同时在⊙M和矩形ABCD内部，求a的取值范围；
（3）过点B作⊙M的切线交边CD于F点，当PF∥AD时，判断直线CE与y轴的交点是否在抛物线上，并说明理由．

查看习题详情和答案>>

如图，在一个等边三角形EFG的内部做一个矩形ABCD，其中等边三角形的边长为40 cm，点C和点D分别在边EF、EG上．

(1)如果设矩形的一边AB＝x cm，那么AD的长度如何表示？

(2)设矩形的面积为y cm，当x取何值时，y的值最大，最大值是多少？

(提示：过点E作EM⊥GF，交CD于点N)

(1)EM的长为________cm．

(2)由DC∥GF，得△________∽△________．

所以DC∶GF＝EN∶EM．

(3)设矩形的一边AB＝x cm，则x∶40＝(EM－AD)∶EM，解得AD＝________．

(4)y与x之间的表达式是________．

(5)因为a________0，所以y有最________值．当x＝________时，矩形的面积有最大值，最大值是________．

析一析：(1)先求出EM的长；

(2)由DC∥GF可以得出两个三角形相似；

(3)利用相似三角形的性质，求出AD的长；

(4)由矩形的面积＝AD·AB，可以求出y与x之间的关系式；

(5)利用y与x之间的关系式可以解答第(2)问吗？试完成下面的解答过程．

查看习题详情和答案>>

如图1，在平面直角坐标系中，已知点

正半轴上，且

个单位的速度运动，设运动时间为秒．点M、N在

是等边三角形．
【小题1】求点B的坐标
【小题2】求等边

的边长（用的代数式表示），并求出当等边

运动到与原点

重合时的值；
【小题3】如果取

内部作如图2所示的矩形

上．设等边

重叠部分的面积为

，请求出当

与的函数关系式，并求出

的最大值．

查看习题详情和答案>>