题目内容
如图,在一个等边三角形EFG的内部做一个矩形ABCD,其中等边三角形的边长为40 cm,点C和点D分别在边EF、EG上.

(1)如果设矩形的一边AB=x cm,那么AD的长度如何表示?
(2)设矩形的面积为y cm,当x取何值时,y的值最大,最大值是多少?
(提示:过点E作EM⊥GF,交CD于点N)
(1)EM的长为________cm.
(2)由DC∥GF,得△________∽△________.
所以DC∶GF=EN∶EM.
(3)设矩形的一边AB=x cm,则x∶40=(EM-AD)∶EM,解得AD=________.
(4)y与x之间的表达式是________.
(5)因为a________0,所以y有最________值.当x=________时,矩形的面积有最大值,最大值是________.
析一析:(1)先求出EM的长;
(2)由DC∥GF可以得出两个三角形相似;
(3)利用相似三角形的性质,求出AD的长;
(4)由矩形的面积=AD·AB,可以求出y与x之间的关系式;
(5)利用y与x之间的关系式可以解答第(2)问吗?试完成下面的解答过程.
答案:
解析:
解析:
(1)20![]() ;
;
(2)DEC,GEF;
(3)![]() ;
;
(4)y=![]() ;
;
(5)<,大,20,200![]() .
.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 如图,把一个等边三角形的顶点放置在正六边形的中心O点,请你借助这个等边三角形的角,以角为工具等分正六边形的面积,等分的情况分别为
如图,把一个等边三角形的顶点放置在正六边形的中心O点,请你借助这个等边三角形的角,以角为工具等分正六边形的面积,等分的情况分别为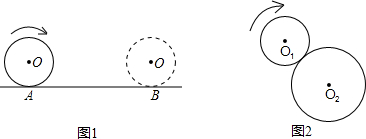
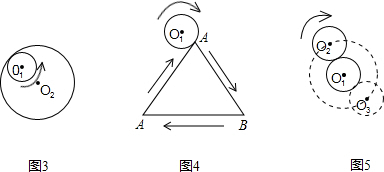
 在边框
在边框 上爬行(
上爬行( ,
, 端点除外),设甲虫
端点除外),设甲虫 ,等边三角形
,等边三角形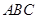 的高为
的高为 ,则
,则 (B)
(B)
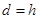 (D)无法确定
(D)无法确定