摘要:4.已知:.且.则的值等于A.5或-5 B.-5或-l C.5或-l D.1或-l
网址:http://m.1010jiajiao.com/timu_id_682010[举报]
已知:如图,直线y=-x+2与两坐标轴分别交与点A、B,点P是线段AB上的点,且坐标为(1,m),将一块三角板绕着点P旋转,三角板的两直角边分别与x轴、y轴相交,交点分别为点D、点E,图①、图②、图③是旋转三角板得到的图形中的3种情况,请你研究:
(1)在图①中,PE⊥y轴,则m=
(2)当三角板旋转到图②或图③的位置时,请你猜想线段PE和PD之间有什么数量关系?并任选其中一个图形加以证明;
(3)三角板绕点P旋转,△PAD是否能成为等腰三角形?若能,请直接写出点D坐标所有的可能情况;若不能,请说明理由.

查看习题详情和答案>>
(1)在图①中,PE⊥y轴,则m=
1
1
,PE:PD的值等于1
1
;(2)当三角板旋转到图②或图③的位置时,请你猜想线段PE和PD之间有什么数量关系?并任选其中一个图形加以证明;
(3)三角板绕点P旋转,△PAD是否能成为等腰三角形?若能,请直接写出点D坐标所有的可能情况;若不能,请说明理由.

阅读以下的材料:
如果两个正数a,b,即a>0,b>0,则有下面的不等式: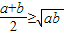 当且仅当a=b时取到等号
当且仅当a=b时取到等号
我们把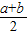 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把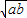 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
例:已知x>0,求函数 的最小值.
的最小值.
解:另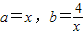 ,则有
,则有 ,得
,得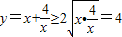 ,当且仅当
,当且仅当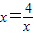 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.
根据上面回答下列问题
①已知x>0,则当x=______ 查看习题详情和答案>>
如果两个正数a,b,即a>0,b>0,则有下面的不等式:
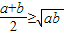 当且仅当a=b时取到等号
当且仅当a=b时取到等号我们把
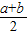 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把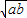 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:例:已知x>0,求函数
 的最小值.
的最小值.解:另
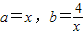 ,则有
,则有 ,得
,得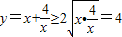 ,当且仅当
,当且仅当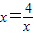 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.根据上面回答下列问题
①已知x>0,则当x=______ 查看习题详情和答案>>
阅读以下的材料:
如果两个正数a,b,即a>0,b>0,则有下面的不等式: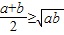 当且仅当a=b时取到等号
当且仅当a=b时取到等号
我们把 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把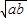 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
例:已知x>0,求函数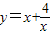 的最小值.
的最小值.
解:另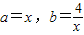 ,则有
,则有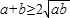 ,得
,得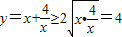 ,当且仅当
,当且仅当 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.
根据上面回答下列问题
①已知x>0,则当x=______ 查看习题详情和答案>>
如果两个正数a,b,即a>0,b>0,则有下面的不等式:
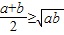 当且仅当a=b时取到等号
当且仅当a=b时取到等号我们把
 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把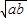 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:例:已知x>0,求函数
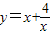 的最小值.
的最小值.解:另
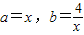 ,则有
,则有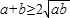 ,得
,得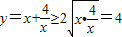 ,当且仅当
,当且仅当 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.根据上面回答下列问题
①已知x>0,则当x=______ 查看习题详情和答案>>
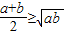 当且仅当a=b时取到等号
当且仅当a=b时取到等号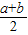 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把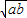 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子: 的最小值.
的最小值. ,则有
,则有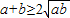 ,得
,得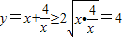 ,当且仅当
,当且仅当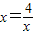 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2. 当且仅当a=b时取到等号
当且仅当a=b时取到等号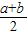 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把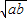 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子: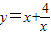 的最小值.
的最小值.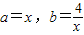 ,则有
,则有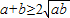 ,得
,得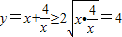 ,当且仅当
,当且仅当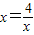 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.