题目内容
阅读以下的材料:如果两个正数a,b,即a>0,b>0,则有下面的不等式:
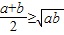 当且仅当a=b时取到等号
当且仅当a=b时取到等号我们把
 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把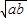 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:例:已知x>0,求函数
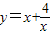 的最小值.
的最小值.解:另
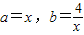 ,则有
,则有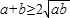 ,得
,得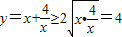 ,当且仅当
,当且仅当 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.根据上面回答下列问题
①已知x>0,则当x=______
【答案】分析:根据阅读材料可以得到两个正数的算术平均数一定大于或等于几何平均数.
(1)令a=2x,b= ,这两个数都是正数,根据:
,这两个数都是正数,根据: 就可以直接得到结果.
就可以直接得到结果.
(2)设这个矩形的长为x米,则宽=面积÷长,即宽= 米,则所用的篱笆总长为2倍的长+2倍的宽,本题就可以转化为两个负数的和的问题,从而根据:
米,则所用的篱笆总长为2倍的长+2倍的宽,本题就可以转化为两个负数的和的问题,从而根据: 求解.
求解.
(3)将原函数变为: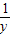 =
= =x+
=x+ -2,则原函数的最大值,即为现在函数的最小值.
-2,则原函数的最大值,即为现在函数的最小值.
解答:解:①已知x>0,得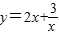
 =
= ,当仅当2x=
,当仅当2x= 时,即x=
时,即x= 时,函数
时,函数 取到最小值,最小值为
取到最小值,最小值为 ;
;
则当x= 时,函数
时,函数 取到最小值,最小值为
取到最小值,最小值为 ;
;
②设这个矩形的长为x米,则宽为 米,所用的篱笆总长为y米,
米,所用的篱笆总长为y米,
根据题意得:y=2x+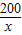
由上述性质知:
∵x>0
∴2x+ ≥40
≥40
此时,2x=
∴x=10
答:当这个矩形的长、宽各为10米时,所用的篱笆最短,最短的篱笆是40米;
③令 =
=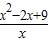 =x+
=x+ -2≥4,
-2≥4,
当且仅当x= 时,
时,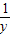 取最小值为4,
取最小值为4,
∴当x=3时,y最大= .
.
点评:本题是阅读型问题,解题的关键是读懂题目中给出的已给信息,理解阅读材料介绍的知识,主要培养自学能力.
(1)令a=2x,b=
 ,这两个数都是正数,根据:
,这两个数都是正数,根据: 就可以直接得到结果.
就可以直接得到结果.(2)设这个矩形的长为x米,则宽=面积÷长,即宽=
 米,则所用的篱笆总长为2倍的长+2倍的宽,本题就可以转化为两个负数的和的问题,从而根据:
米,则所用的篱笆总长为2倍的长+2倍的宽,本题就可以转化为两个负数的和的问题,从而根据: 求解.
求解.(3)将原函数变为:
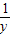 =
= =x+
=x+ -2,则原函数的最大值,即为现在函数的最小值.
-2,则原函数的最大值,即为现在函数的最小值.解答:解:①已知x>0,得
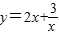
 =
= ,当仅当2x=
,当仅当2x= 时,即x=
时,即x= 时,函数
时,函数 取到最小值,最小值为
取到最小值,最小值为 ;
;则当x=
 时,函数
时,函数 取到最小值,最小值为
取到最小值,最小值为 ;
;②设这个矩形的长为x米,则宽为
 米,所用的篱笆总长为y米,
米,所用的篱笆总长为y米,根据题意得:y=2x+
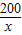
由上述性质知:
∵x>0
∴2x+
 ≥40
≥40此时,2x=

∴x=10
答:当这个矩形的长、宽各为10米时,所用的篱笆最短,最短的篱笆是40米;
③令
 =
=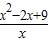 =x+
=x+ -2≥4,
-2≥4,当且仅当x=
 时,
时,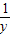 取最小值为4,
取最小值为4,∴当x=3时,y最大=
 .
.点评:本题是阅读型问题,解题的关键是读懂题目中给出的已给信息,理解阅读材料介绍的知识,主要培养自学能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
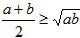 当且仅当a=b时取到等号,我们把
当且仅当a=b时取到等号,我们把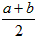 叫做正数的算术平均数,把
叫做正数的算术平均数,把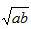 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子: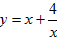 的最小值。
的最小值。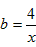 ,则有
,则有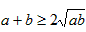 ,得
,得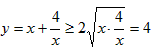 ,当且仅当
,当且仅当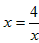 时,即x=2时,函数有最小值,最小值为2。
时,即x=2时,函数有最小值,最小值为2。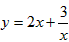 取到最小值,最小值为______;
取到最小值,最小值为______;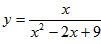 取到最大值,最大值为多少?
取到最大值,最大值为多少? 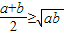 当且仅当a=b时取到等号
当且仅当a=b时取到等号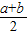 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把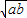 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子: 的最小值.
的最小值.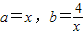 ,则有
,则有 ,得
,得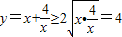 ,当且仅当
,当且仅当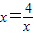 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.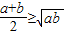 当且仅当a=b时取到等号
当且仅当a=b时取到等号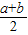 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把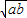 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子:
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具,下面举一例子: 的最小值.
的最小值. ,则有
,则有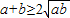 ,得
,得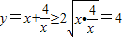 ,当且仅当
,当且仅当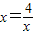 时,即x=2时,函数有最小值,最小值为2.
时,即x=2时,函数有最小值,最小值为2.