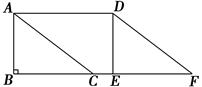
摘要:11.如图.△ABC中.∠B=90°.AB=6.BC=8.将△ABC沿DE折叠.使点C落在AB边上的C’处.并且C’D∥BC.则CD的长是
网址:http://m.1010jiajiao.com/timu_id_679140[举报]
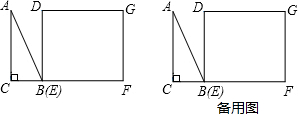 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°;四边形DEFG为矩形,DE=2
如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°;四边形DEFG为矩形,DE=2| 3 |
(1)求边AC的长;
(2)求y 与x 的函数关系式;
(3)当Rt△ABC移动至重叠部分的面积为y=
| 3 |
| 2 |
| 3 |
(4)点P从点D出发,沿矩形DEFG的边DE、EF、FG运动到点G停止.其中点P在DE边上的速度为2
| 3 |
| 3 |
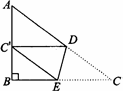
如图,△ABC中,AB=AC=
,∠BAC=90°,DE经过点A,且DE⊥BC,垂足为E,∠DCE=60°.
(1)以点E为中心,逆时针旋转△CDE,使旋转后得到的△C′D′E的边C′D′恰好经过点A,求此时旋转角的大小;
(2)在(1)的情况下,将△C′D′E沿BC向右平移t(0<t<1),设平移后的图形与△ABC重叠部分面积为S,求S与t的函数关系式,并直接写出t的取值范围.
查看习题详情和答案>>
| 2 |
(1)以点E为中心,逆时针旋转△CDE,使旋转后得到的△C′D′E的边C′D′恰好经过点A,求此时旋转角的大小;
(2)在(1)的情况下,将△C′D′E沿BC向右平移t(0<t<1),设平移后的图形与△ABC重叠部分面积为S,求S与t的函数关系式,并直接写出t的取值范围.

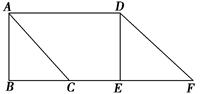
如图,△ABC中,∠B=90°,AB=6 cm,BC=8 cm.将△ABC沿射线BC方向平移10 cm,得到△DEF,A,B,C的对应点分别是D,E,F,连结AD.求证:四边形ACFD是菱形.