摘要:附加题:在第26题中.抛物线的解析式和点D的坐标不变.当x > 0时.在直线(0 < k < 1)和这条抛物线上.是否分别存在点P和点Q.使四边形DOPQ为以OD为底的等腰梯形.若存在.求点P.Q的坐标,若不存在.说明理由.
网址:http://m.1010jiajiao.com/timu_id_676799[举报]
如图,直线AB交x轴于点A(2,0),交抛物线![]() 于点B(1,
于点B(1,![]() ),点C到△OAB各顶点的距离相等,直线AC交y轴于点D.当x > 0时,在直线OC和抛物线
),点C到△OAB各顶点的距离相等,直线AC交y轴于点D.当x > 0时,在直线OC和抛物线![]() 上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由.
上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由.

附加题:在上题中,抛物线的解析式和点D的坐标不变(如下图).当x > 0时,在直线![]() (0 < k < 1)和这条抛物线上,是否分别存在点P和点Q,使四边形DOPQ为以OD为底的等腰梯形.若存在,求点P、Q的坐标;若不存在,说明理由.
(0 < k < 1)和这条抛物线上,是否分别存在点P和点Q,使四边形DOPQ为以OD为底的等腰梯形.若存在,求点P、Q的坐标;若不存在,说明理由.

(1)如图1,直线AB交x轴于点A(2,0),交抛物线y=ax2于点B(1,
),点C到△OAB各顶点的距离相等,直线AC交y轴于点D.当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由.
(2)在(1)题中,抛物线的解析式和点D的坐标不变(如图2).当x>0时,在直线y=kx(0<k<1)和这条抛物线上,是否分别存在点P和点Q,使四边形DOPQ为以OD为底的等腰梯形.若存在,求点P、Q的坐标;若不存在,说明理由.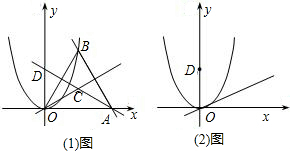 查看习题详情和答案>>
查看习题详情和答案>>
| 3 |
(2)在(1)题中,抛物线的解析式和点D的坐标不变(如图2).当x>0时,在直线y=kx(0<k<1)和这条抛物线上,是否分别存在点P和点Q,使四边形DOPQ为以OD为底的等腰梯形.若存在,求点P、Q的坐标;若不存在,说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 ),点C到△OAB各顶点的距离相等,直线AC交y轴于点D.当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由.
),点C到△OAB各顶点的距离相等,直线AC交y轴于点D.当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由.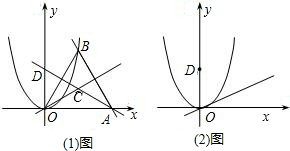
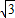 ),点C到△OAB各顶点的距离相等,直线AC交y轴于点D.当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由.
),点C到△OAB各顶点的距离相等,直线AC交y轴于点D.当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,求点P、Q的坐标;若不存在,说明理由.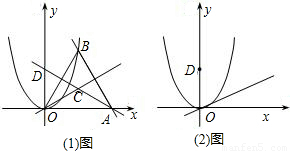
 C的周长的最小值.
C的周长的最小值.