题目内容
(1)如图1,直线AB交x轴于点A(2,0),交抛物线y=ax2于点B(1,| 3 |
(2)在(1)题中,抛物线的解析式和点D的坐标不变(如图2).当x>0时,在直线y=kx(0<k<1)和这条抛物线上,是否分别存在点P和点Q,使四边形DOPQ为以OD为底的等腰梯形.若存在,求点P、Q的坐标;若不存在,说明理由.
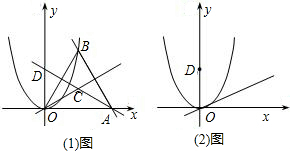
分析:利用已知可以首先求出AD直线的解析式,再利用特殊梯形只有直角梯形与等腰梯形,分别讨论可以求出.
点评:此题主要考查了一次函数与二次函数的综合应用,并且利用等边三角形的性质,综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
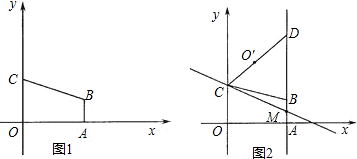
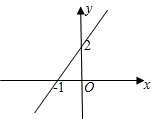 如图,该直线是某个一次函数的图象,则此函数的解析式为
如图,该直线是某个一次函数的图象,则此函数的解析式为
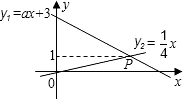 如图,两直线y1=ax+3与y2=
如图,两直线y1=ax+3与y2=