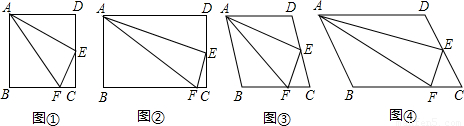
摘要:23.如图11-1.小明在研究正方形ABCD的有关问题时.得出:“在正方形ABCD中.如果点E是CD的中点.点F是BC边上的一点.且∠FAE =∠EAD.那么EF⊥AE .他又将“正方形 改为“矩形 .“菱形 和“任意平行四边形 .其他条件不变.发现仍然有“EF⊥AE 的结论.你同意小明的观点吗?若同意.请结合图11-4加以证明,若不同意.请说明理由.
网址:http://m.1010jiajiao.com/timu_id_676790[举报]
27、如图①,小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”.他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件不变,发现仍然有“EF⊥AE”结论.
你同意小明的观点吗?同意,请结合图④加以证明;若不同意,请说明理由.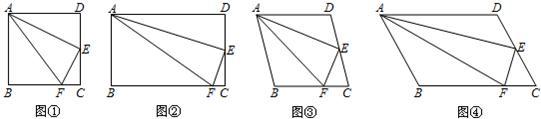
查看习题详情和答案>>
你同意小明的观点吗?同意,请结合图④加以证明;若不同意,请说明理由.

(2007•大连)如图①,小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”.他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件不变,发现仍然有“EF⊥AE”结论.
你同意小明的观点吗?同意,请结合图④加以证明;若不同意,请说明理由.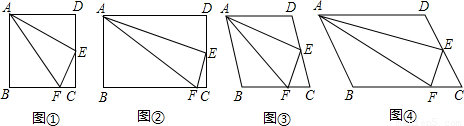
查看习题详情和答案>>
你同意小明的观点吗?同意,请结合图④加以证明;若不同意,请说明理由.

查看习题详情和答案>>
(2007•大连)如图①,小明在研究正方形ABCD的有关问题时,得出:“在正方形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,那么EF⊥AE”.他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件不变,发现仍然有“EF⊥AE”结论.
你同意小明的观点吗?同意,请结合图④加以证明;若不同意,请说明理由.
查看习题详情和答案>>
你同意小明的观点吗?同意,请结合图④加以证明;若不同意,请说明理由.

查看习题详情和答案>>