Question

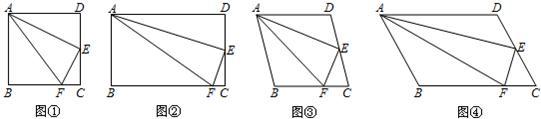
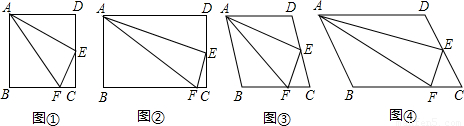
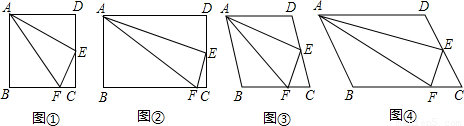
如图，小明在研究正方形ABCD的有关问题时，得出：“在正方形ABCD中，如果点E是CD的中点，点F是BC边上的一点，且∠FAE =∠EAD，那么EF⊥AE”．他又将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图2、图3、图4)，其他条件不变，发现仍然有“EF⊥AE”的结论．

你同意小明的观点吗？若同意，请结合图1－4加以证明；若不同意，请说明理由．

Answer 1

解:同意.

方法一:

证明:如图(略)①,延长AE交BC的延长线于点G.

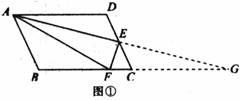
∵四边形ABCD是平行四边形,

∴AD//BC, ∴∠D=∠ECG,

∵E为DC的中点, ∴DE=EC,

又∵∠DEA=∠CEG, ∴△ADE≌△GCE(ASA)

∴AE=GE, ∠DAE=∠G

∵∠FAE=∠DAE, ∴∠FAE=∠G.

∴FA=FG.

∴EF⊥AE

方法二:

证明: 如图②,在AF上截取AG=AD,连接EG、GC.

∵∠FAE=∠EAD,AE=AE, ∴△AEG≌△AED(SAS).

∴DE=GE, ∠AGE=∠D, ∠1=∠2.

∵点E是DC的中点，∴EC=DE, ∴EC=GE.

∵四边形ABCD是平行四边形, ∴AD//BC, ∴∠BCD+∠D=180°.

∵∠EGF+∠AGE=180°, ∴∠BCD=∠EGF

∵EG=EC, ∴∠EGC=∠ECG. ∴∠FGC=∠FCG. ∴GF=FC.

又∵EF=EF, ∴△GEF≌△CEF(SSS)

∴∠3=∠4.

∴∠AEF=∠2+∠3=(∠1+∠2+∠3+∠4)=×180°=90°.

∴EF⊥AE