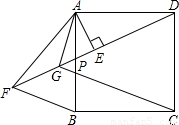
摘要：在边长为1的正方形ABCD中.E是AB的中点.CF⊥DE.F为垂足． (1) △CDF与△DEA是否相似?说明理由,(2) 求CF的长．
网址：http://m.1010jiajiao.com/timu_id_653246[举报]
正方形ABCD中，P为AB边上任一点，AE⊥DP于E，点F在DP的延长线上，且DE=EF，连接AF、BF，∠BAF的平分线交DF于G，连接GC．（1）求证：△AEG是等腰直角三角形；
（2）求证：AG+CG=
| 2 |
（3）若AB=2，P为AB的中点，求BF的长．
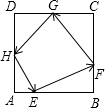如图，在边长为1正方形ABCD中，E、F、G分别是AB、BC、CD、DA上的点，3AE=EB，有一只蚂蚁从E点出发，经过F、G、H，最后回点E点，则蚂蚁所走的最小路程是（ ）| A、2 | ||
| B、4 | ||
C、2
| ||
D、3
|
正方形ABCD中，点E、F分别是边AD、AB的中点，连接EF.
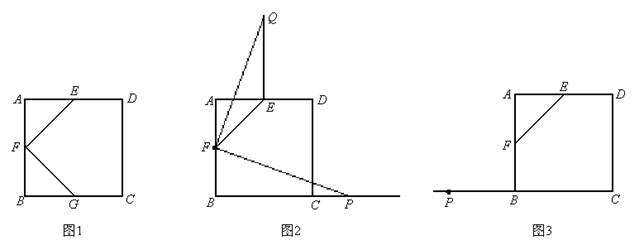
（1）如图1，若点G是边BC的中点，连接FG，则EF与FG关系为： ；
（2）如图2，若点P为BC延长线上一动点，连接FP，将线段FP以点F为旋转中心,逆时针旋转900，得到线段FQ，连接EQ，请猜想EF、EQ、BP三者之间的数量关系，并证明你的结论；
（3）若点P为CB延长线上一动点，按照（2）中的作法，在图3中补全图形，并直接写出EF、EQ、BP三者之间的数量关系： .
查看习题详情和答案>>
；
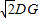