题目内容
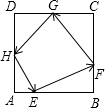 如图,在边长为1正方形ABCD中,E、F、G分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是( )
如图,在边长为1正方形ABCD中,E、F、G分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是( )| A、2 | ||
| B、4 | ||
C、2
| ||
D、3
|
分析:延长DC到D',使CD=CD',G对应位置为G',则FG=FG',作D'A'⊥CD',D'A'=DA,H对应的位置为H',则G'H'=GH,再作A'B'⊥D'A',E的对应位置为E',则H'E'=HE.由两点之间线段最短可知当E、F、G'、H'、E'在一条直线上时路程最小,再延长AB至K使BK=AB,连接E′K,利用勾股定理即可求出EE′的长.
解答:解:延长DC到D',使CD=CD',G关于C对称点为G',则FG=FG',
同样作D'A'⊥CD',D'A'=DA,H对应的位置为H',则G'H'=GH,
再作A'B'⊥D'A',E的对应位置为E',
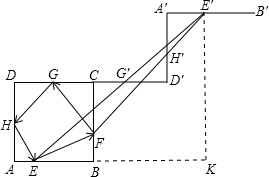
则H'E'=HE.
容易看出,当E、F、G'、H'、E'在一条直线上时路程最小,
最小路程为EE'=
=
=2
.
故选C.
同样作D'A'⊥CD',D'A'=DA,H对应的位置为H',则G'H'=GH,
再作A'B'⊥D'A',E的对应位置为E',

则H'E'=HE.
容易看出,当E、F、G'、H'、E'在一条直线上时路程最小,
最小路程为EE'=
| (2AB)2+(2BC)2 |
| 4+4 |
| 2 |
故选C.
点评:本题考查的是最短路线问题,解答此题的关键是画出图形,根据两点之间线段最短的道理求解.

练习册系列答案
相关题目
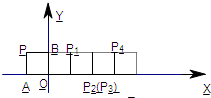 18、如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2008的位置,则P2008的横坐标X2008=
18、如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2008的位置,则P2008的横坐标X2008=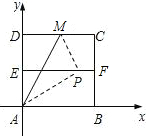 D、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.
D、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.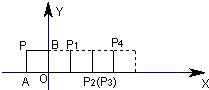 19、如图,将边长为1的正方形OAPB沿轴正方向连续翻转2007次,点P依次落在点P1,P2,P3,P4,…,P2007的位置,则P2007的横坐标x2007=( )
19、如图,将边长为1的正方形OAPB沿轴正方向连续翻转2007次,点P依次落在点P1,P2,P3,P4,…,P2007的位置,则P2007的横坐标x2007=( )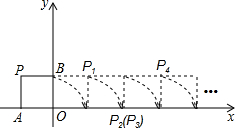 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,P4,…,P2008的位置,则P2008的坐标为
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,P4,…,P2008的位置,则P2008的坐标为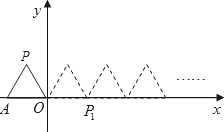 如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2012的位置,则点P2012的横坐标为
如图,将边长为1的正三角形OAP沿x轴正方向连续翻转2008次,点P依次落在点P1,P2,P3,…,P2012的位置,则点P2012的横坐标为