摘要:黑色小正方形个数 - 正方形边长2468-
网址:http://m.1010jiajiao.com/timu_id_653104[举报]
25、如图每个正方形是由边长为1的小正方形组成.
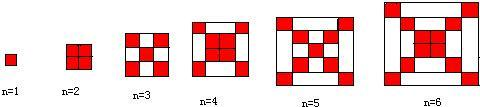
(1)观察图形,请填与下列表格:
(2)在边长为n(n≥1)的正方形中,设红色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1,若存在,请写出n的值,若不存在,请说明理由.
查看习题详情和答案>>

(1)观察图形,请填与下列表格:
| 正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
| 黑色小正方形个数 | … |
| 正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
| 黑色小正方形个数 | … |
如图,每个大正方形是由边长为1的小正方形组成。观察以上图形,完成下列填空:

(1)猜想:当n为奇数时,图n中黑色小正方形的个数为 ,当n为偶数时,图n中黑色小正方形的个数为 ;
(2)在边长为偶数的正方形中,白色小正方形的个数是黑色小正方形个数的4倍,求这个正方形的边长。

(1)猜想:当n为奇数时,图n中黑色小正方形的个数为 ,当n为偶数时,图n中黑色小正方形的个数为 ;
(2)在边长为偶数的正方形中,白色小正方形的个数是黑色小正方形个数的4倍,求这个正方形的边长。
在下图中,每个正方形由边长为1 的小正方形组成:
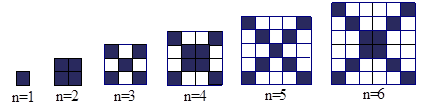
1.观察图形,请填写下列表格:
| 正方形边长 | 1 | 3 | 5 | 7 | … |
|
| 黑色小正方形个数 |
|
|
|
| … |
|
| 正方形边长 | 2 | 4 | 6 | 8 | … |
|
| 黑色小正方形个数 |
|
|
|
| … |
|
2.在边长为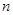 (n≥1)的正方形中,设黑色小正方形的个数为
(n≥1)的正方形中,设黑色小正方形的个数为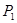 ,白色小正方形的个数为
,白色小正方形的个数为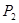 ,问是否存在偶数
,问是否存在偶数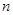 ,使
,使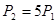 ?若存在,请写出
?若存在,请写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>
在下图中,每个正方形由边长为1 的小正方形组成: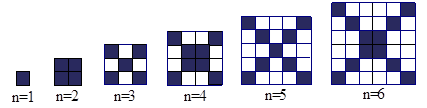
【小题1】观察图形,请填写下列表格:
| 正方形边长 | 1 | 3 | 5 | 7 | … | 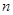 (奇数) (奇数) |
| 黑色小正方形个数 | | | | | … | |
| 正方形边长 | 2 | 4 | 6 | 8 | … | 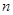 (偶数) (偶数) |
| 黑色小正方形个数 | | | | | … | |
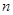 (n≥1)的正方形中,设黑色小正方形的个数为
(n≥1)的正方形中,设黑色小正方形的个数为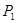 ,白色小正方形的个数为
,白色小正方形的个数为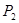 ,问是否存在偶数
,问是否存在偶数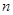 ,使
,使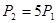 ?若存在,请写出
?若存在,请写出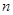 的值;若不存在,请说明理由.
查看习题详情和答案>>
的值;若不存在,请说明理由.
查看习题详情和答案>>
在下图中,每个正方形由边长为1 的小正方形组成:
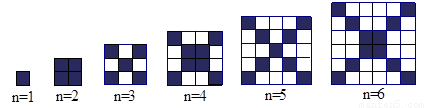
1.观察图形,请填写下列表格:
|
正方形边长[来源:] |
1 |
3 |
5 |
7 |
… |
|
|
黑色小正方形个数 |
|
|
|
|
… |
|
|
正方形边长 |
2 |
4 |
6 |
8 |
… |
|
|
黑色小正方形个数 |
|
|
|
|
… |
|
2.在边长为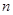 (n≥1)的正方形中,设黑色小正方形的个数为
(n≥1)的正方形中,设黑色小正方形的个数为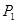 ,白色小正方形的个数为
,白色小正方形的个数为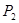 ,问是否存在偶数
,问是否存在偶数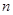 ,使
,使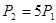 ?若存在,请写出
?若存在,请写出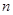 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>