要证，只需证，即需，即需证，即证35>11，因为35>11显然成立，所以原不等式成立。以上证明运用了

A．比较法           B．综合法           C．分析法           D．反证法

当P为何值时，对任意实数x,不等式－9＜≤6恒   成立.

将原不等式等价转化为一元二次不等式组.

已知函数其中为自然对数的底数， .(Ⅰ)设，求函数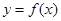的最值；（Ⅱ）若对于任意的，都有成立，求的取值范围.

【解析】第一问中，当时，，．结合表格和导数的知识判定单调性和极值，进而得到最值。

第二问中，∵，，      

∴原不等式等价于：,

即, 亦即

分离参数的思想求解参数的范围

解：（Ⅰ)当时，，．

当在上变化时，，的变化情况如下表：

∴时，，．

(Ⅱ)∵，，      

∴原不等式等价于：,

即, 亦即．

∴对于任意的，原不等式恒成立,等价于对恒成立,

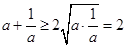∵对于任意的时, （当且仅当时取等号）．

∴只需，即，解之得或.

因此，的取值范围是