摘要:25.如图.直角坐标系内的矩形ABCD中顶点A的坐标为(0.3).BC=2AB.P为AD边上一动点.以点P为圆心作⊙P.与对角线AC相切于点F.过P.F作直线.交BC边上于点E .当点P运动到点位置时.直线恰好经过点B.此时直线的解析式是 .(1) 求BC.AP1的长,
网址:http://m.1010jiajiao.com/timu_id_648281[举报]
如图,直角坐标系内的矩形ABCD中顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P,与对角线AC相切于点F,过P、F作直线l,交BC边上于点E .当点P运动到点P1位置时,直线l恰好经过点B,此时直线的解析式是y=2x+1 .
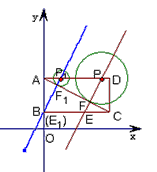
(1)求BC、AP1的长;
(2)设AP=m,梯形PECD的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
(3)以点E为圆心作⊙E,与x轴相切 .试探究并猜想⊙P和⊙E有哪几种不同的位置关系,并求出AP相应的取值范围.
查看习题详情和答案>>
(2)设AP=m,梯形PECD的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
(3)以点E为圆心作⊙E,与x轴相切 .试探究并猜想⊙P和⊙E有哪几种不同的位置关系,并求出AP相应的取值范围.
在平面直角坐标系中,点C为反比例函数y=
(k>0)在第一象限内图象上一点,以点A(-2,-2)和C为顶点的矩形ABCD中,AB∥CD∥x轴,AB交y轴于点Q,CD交y轴于点M,BC∥DA∥y轴于点I,DA交x轴于点N,矩形ABCD被坐标轴分成的四个四边形的面积分别为S1,S2,S3,S4(如图1所示),已知S1=3S3,
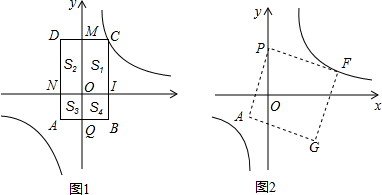
(1)求k的值;
(2)S2•S4的值为
(3)P(0,n)为y轴上一点,以AP为边作正方形APFG(A,P,F,G的位置依次为顺时针方向排列),当点F或G恰好落在反比例函数y=
的图象上(示意图如图2所示)时,求所有满足条件的n的值.
查看习题详情和答案>>
| k |
| x |

(1)求k的值;
(2)S2•S4的值为
48
48
;(3)P(0,n)为y轴上一点,以AP为边作正方形APFG(A,P,F,G的位置依次为顺时针方向排列),当点F或G恰好落在反比例函数y=
| k |
| x |
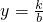 (k>0)在第一象限内图象上一点,以点A(-2,-2)和C为顶点的矩形ABCD中,AB∥CD∥x轴,AB交y轴于点Q,CD交y轴于点M,BC∥DA∥y轴于点I,DA交x轴于点N,矩形ABCD被坐标轴分成的四个四边形的面积分别为S1,S2,S3,S4(如图1所示),已知S1=3S3,
(k>0)在第一象限内图象上一点,以点A(-2,-2)和C为顶点的矩形ABCD中,AB∥CD∥x轴,AB交y轴于点Q,CD交y轴于点M,BC∥DA∥y轴于点I,DA交x轴于点N,矩形ABCD被坐标轴分成的四个四边形的面积分别为S1,S2,S3,S4(如图1所示),已知S1=3S3,
 的图象上(示意图如图2所示)时,求所有满足条件的n的值.
的图象上(示意图如图2所示)时,求所有满足条件的n的值.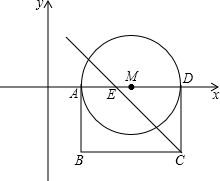 顶点为P.
顶点为P. 顶点为P.
顶点为P.