题目内容
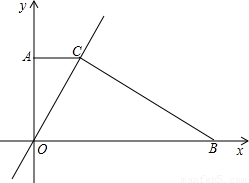
如图,直角坐标系内的矩形ABCD中顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P,与对角线AC相切于点F,过P、F作直线l,交BC边上于点E .当点P运动到点P1位置时,直线l恰好经过点B,此时直线的解析式是y=2x+1 .
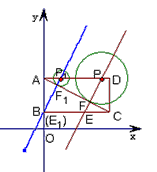
(1)求BC、AP1的长;
(2)设AP=m,梯形PECD的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
(3)以点E为圆心作⊙E,与x轴相切 .试探究并猜想⊙P和⊙E有哪几种不同的位置关系,并求出AP相应的取值范围.
(2)设AP=m,梯形PECD的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
(3)以点E为圆心作⊙E,与x轴相切 .试探究并猜想⊙P和⊙E有哪几种不同的位置关系,并求出AP相应的取值范围.
解:(1)由y=2x+1可知, 当x=0时 ,y=1
∴ 点B(0,1) ∵点A(0,3)
∴AB=2 又 BC=2AB ∴ BC=4
∵点P1在直线y=2x+1和AD边上,又AD // x轴 , ∴可设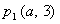
则 3=2a+1 即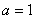 ∴
∴  ∴AP1=1 ;
∴AP1=1 ;
(2)∵AP=m AD=4 AP1=1
∴PD = 4-m P1P = m-1
又P1P//BE,P1B//PE, ∴P1PEB是平行四边形.
∴BE=P1P ∴EC = 4-(m-1) = 5-m
∴S= [(4-m)+(5-m)]×2 = 9-2m 1≤m<4;
[(4-m)+(5-m)]×2 = 9-2m 1≤m<4;
(3)当⊙E与x轴及⊙P外切时,EF=1, ∵ △CFE∽△CBA
∴ ∴
∴ 即EC=
即EC=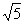
∴BE=4- 即m-1=4-
即m-1=4- 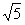 ∴m=5-
∴m=5- 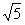
∴当m=5-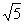 时, ⊙P与⊙E外切;
时, ⊙P与⊙E外切;
当1≤m<5-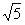 时, ⊙P与⊙E外离;
时, ⊙P与⊙E外离;
当5- <m<4时, ⊙P与⊙E相交 。
<m<4时, ⊙P与⊙E相交 。
∴ 点B(0,1) ∵点A(0,3)
∴AB=2 又 BC=2AB ∴ BC=4
∵点P1在直线y=2x+1和AD边上,又AD // x轴 , ∴可设
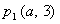
则 3=2a+1 即
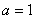 ∴
∴  ∴AP1=1 ;
∴AP1=1 ;(2)∵AP=m AD=4 AP1=1
∴PD = 4-m P1P = m-1
又P1P//BE,P1B//PE, ∴P1PEB是平行四边形.
∴BE=P1P ∴EC = 4-(m-1) = 5-m
∴S=
 [(4-m)+(5-m)]×2 = 9-2m 1≤m<4;
[(4-m)+(5-m)]×2 = 9-2m 1≤m<4;(3)当⊙E与x轴及⊙P外切时,EF=1, ∵ △CFE∽△CBA
∴
 ∴
∴ 即EC=
即EC=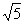
∴BE=4-
 即m-1=4-
即m-1=4- 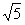 ∴m=5-
∴m=5- 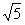
∴当m=5-
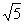 时, ⊙P与⊙E外切;
时, ⊙P与⊙E外切; 当1≤m<5-
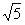 时, ⊙P与⊙E外离;
时, ⊙P与⊙E外离;当5-
 <m<4时, ⊙P与⊙E相交 。
<m<4时, ⊙P与⊙E相交 。
练习册系列答案
相关题目
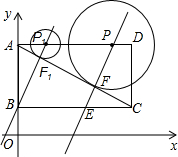 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线L,交BC边于点E,当点P运动到点P1位置时,直线L恰好经过点B,此时直线的解析式是y=2x+1.
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线L,交BC边于点E,当点P运动到点P1位置时,直线L恰好经过点B,此时直线的解析式是y=2x+1. 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为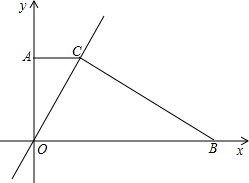
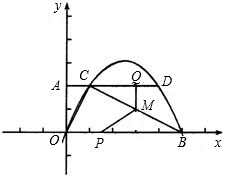
 S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.
S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.