摘要:解析:P点取法总共有9种.由图知直线截距为2时经过的点最多,∴选A.
网址:http://m.1010jiajiao.com/timu_id_64739[举报]
已知双曲线C:
-
=1(a>0,b>0)
(1)若a=4,b=3,过点P(6,3)的动直线l与双曲线C相交于不同两点A,B时,在线段AB上取点Q,满足|
|•|
|=|
|•|
|,求证点Q总在某定直线上.
(2)在双曲线C:
-
=1(a>0,b>0),过双曲线外一点P(m,n)的动直线l与双曲线C相交于不同两点A,B时,在线段AB上取点Q,满足|
|•|
|=|
|•|
|,则点Q在哪条定直线上?
(3)试将该结论推广至其它圆锥曲线上,证明其中的一种情况,并猜想该直线具有的性质. 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(1)若a=4,b=3,过点P(6,3)的动直线l与双曲线C相交于不同两点A,B时,在线段AB上取点Q,满足|
| AP |
| QB |
| AQ |
| PB |
(2)在双曲线C:
| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| QB |
| AQ |
| PB |
(3)试将该结论推广至其它圆锥曲线上,证明其中的一种情况,并猜想该直线具有的性质. 查看习题详情和答案>>
 设双曲线
设双曲线| x2 |
| 4 |
(1)证明:无论P点在什么位置,总有|
| OP |
| OQ |
| OR |
(2)设动点C满足条件:
| AC |
| 1 |
| 2 |
| AQ |
| AR |
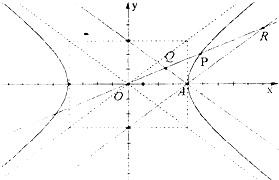 设双曲线
设双曲线| x2 |
| a2 |
| y2 |
| b2 |
(1)证明:无论P点在什么位置,总有|
| OP |
| OQ |
| OR |
(2)若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积,求双曲线离心率的取值范围. 查看习题详情和答案>>
 (2012•浦东新区一模)世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地,如图点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x,x∈[10,20].
(2012•浦东新区一模)世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地,如图点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x,x∈[10,20].