Question

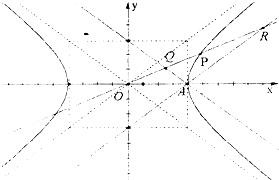设双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)的右顶点为A，P是双曲线上异于顶点的一个动点，从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点．（如图）
（1）证明：无论P点在什么位置，总有|

OP

|2=|

OQ

•

OR

|(O为坐标原点)；
（2）若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积，求双曲线离心率的取值范围．

Answer 1

分析：（1）先求出

OR

、

OQ

的坐标，计算|

OQ

•

OR

|的值，把双曲线方程与OP方程联立解得 |

OP|

2，比较可得|

OP

|2=|

OQ

•

OR

|．
（2）由条件得：

a2b2(1+k2)

b2-a2k2

=4ab，根据k²＞0，得到b＞

a

4

，计算e=

a2+b2 a2

 的范围．

解答：解：（1）设OP的方程为 y=kx，AR的方程为 y=

b

a

(x-a)，
解得 

OR

=(

-ab

ak-b

，

-kab

ak-b

)，同理可得

OQ

=(

ab

ak+b

，

kab

ak+b

)．
∴|

OQ

•

OR

|=|

-ab

ak-b

ab

ak+b

+

-kab

ak-b

kab

ak+b

|=|

a2b2(1+k2)

|a2k2-b2|

．
设

OP

=(m，n)，则由双曲线方程与OP方程联立解得：

m2= a2b2 b2-a2k2 ，n2= k2a2b2 b2-a2k2 ，

∴

| OP |2=m2+n2= a2b2 b2-a2k2 + k2a2b2 b2-a2k2 = a2b2(1+k2) b2-a2k2 ，

 
∵点P在双曲线上，∴b²-a²k²＞0，无论点P在什么位置，总有  |

OP

|2=|

OQ

•

OR

|．
（2）由条件得：

a2b2(1+k2)

b2-a2k2

=4ab，即  k2=

4b2-ab

ab+4a2

＞0，
∴4b＞a，∴e=

c

a

=

a2+b2

a

＞

a2+( a 4 )2

a

=

17

4

，即 e＞

17

4

．

点评：本题考查两个向量的数量积，双曲线的标准方程，以及双曲线的简单性质的应用，式子的变形、化简是解题的难点．