题目内容
Rt△ABC,∠ACB=90°,BC=2,如图1,将△ABC置于坐标系中,使BC边落在y 轴正半轴上,点B位于原点处,点A位于第一象限.将顶点B、C分别在x轴、y轴的正半轴上向右、向下滑动,当点C与原点重合时停止滑动.
(Ⅰ)①如图2,若AC=2,B点右滑的距离OB是1,求C点下滑的距离和AC所在的直线解析式;②如图2,点C继续滑动多远时,C点下滑距离CN与B点右滑距离BM相等;
(Ⅱ)如图3,在滑动的过程中BC的中点P也随之移动,求整个过程中P点移动路径的长度;
(Ⅲ)若AC=
,求滑动的过程中A到原点O的最大距离以及此时点A的坐标.

(Ⅰ)①如图2,若AC=2,B点右滑的距离OB是1,求C点下滑的距离和AC所在的直线解析式;②如图2,点C继续滑动多远时,C点下滑距离CN与B点右滑距离BM相等;
(Ⅱ)如图3,在滑动的过程中BC的中点P也随之移动,求整个过程中P点移动路径的长度;
(Ⅲ)若AC=
| 3 | 4 |

分析:(1)①Rt△OBC中,利用勾股定理算出OC=
=
,可得C点下滑的距离为2-
.利用三角函数的定义算出∠CBO=∠ACy=60°,得到AC的倾斜角为30°,所以AC的斜率为
,进而可得AC所在直线的解析式;
②根据△OBC与△ONM全等,算出ON=OB=1,从而得出CN=
-1,所以继续滑动的距离为
-1时,可使CN=BM;
(2)根据直角三角形的性质得OP=
BC=1,从而得到点P在以O为圆心、半径r=1的圆上运动,由此可得P点的移动路径是圆心角为直角的圆弧,利用弧长公式即可算出移动路径的长度;
(3)利用勾股定理算出AP=
,结合OP=
BC=1,可得当O、P、A三点共线时,点A到原点的距离距离为OP+PA=
达到最大值.然后根据相似三角形的判定与性质算出OH=3AH,在Rt△OHA中利用勾股定理算出AH、OH的长,进而可得点A的坐标.
| BC2-OB2 |
| 3 |
| 3 |
| ||
| 3 |
②根据△OBC与△ONM全等,算出ON=OB=1,从而得出CN=
| 3 |
| 3 |
(2)根据直角三角形的性质得OP=
| 1 |
| 2 |
(3)利用勾股定理算出AP=
| 5 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
解答:解:(1)①如图2,Rt△OBC中,BC=2,OB=1,
根据勾股定理,得OC=
=
,
∴C点下滑的距离d=2-
,
又∵Rt△OBC中,tan∠CBO=
=
,
∴∠CBO=∠ACy=60°,
可得直线AC的倾斜角为90°-60°=30°,AC的斜率为k=tan30°=
.
∵直线AC经过点C(0,
)
∴AC所在的直线解析式为:y=
x+
;
②当C点下滑距离CN与B点右滑距离BM相等时,△OBC≌△ONM,
此时∠CBO=∠MNO=60°,可得ON=OB=1,
∴CN=CO-ON=
-1,
即继续滑动
-1时,可使C点下滑距离CN与B点右滑距离BM相等;
(2)连接OP,则Rt△OBC中,OP是斜边BC上的中线,
∴OP=
BC=1,可得点P在以O为圆心、半径r=1的圆上运动.
由此可得:P点的移动路径是以O为圆心、圆心角等于90°的弧,
其长度为L=
=
;
(3)∵Rt△ACP中,AC=
,PC=
BC=1,
∴AP=
=
=
;
又∵OP=
BC=1,OP、AP都是定长
∴当O、P、A三点共线时,A到原点O的距离最大.最大距离为OP+PA=1+
=
,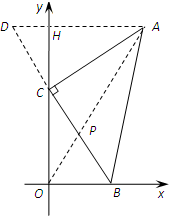
过A作AH⊥y轴,与BC的延长线交于点D,
∵AD∥OB,∴△POB∽△PAD,结合PB=OP得PD=AP=
由此可得DC=PD-CP=
-1=
,
又∵Rt△ACD∽Rt△OHA,AC=
,
∴
=
=
,
∵OA=
,∴OH=3AH,
又∵Rt△OHA中,OA=
=
,
∴AH=
,OH=
,可得点A的坐标(
,
).
根据勾股定理,得OC=
| BC2-OB2 |
| 3 |
∴C点下滑的距离d=2-
| 3 |
又∵Rt△OBC中,tan∠CBO=
| OC |
| OB |
| 3 |
∴∠CBO=∠ACy=60°,
可得直线AC的倾斜角为90°-60°=30°,AC的斜率为k=tan30°=
| ||
| 3 |
∵直线AC经过点C(0,
| 3 |
∴AC所在的直线解析式为:y=
| ||
| 3 |
| 3 |
②当C点下滑距离CN与B点右滑距离BM相等时,△OBC≌△ONM,
此时∠CBO=∠MNO=60°,可得ON=OB=1,
∴CN=CO-ON=
| 3 |
即继续滑动
| 3 |
(2)连接OP,则Rt△OBC中,OP是斜边BC上的中线,
∴OP=
| 1 |
| 2 |
由此可得:P点的移动路径是以O为圆心、圆心角等于90°的弧,
其长度为L=
| 90πr |
| 180 |
| π |
| 2 |
(3)∵Rt△ACP中,AC=
| 3 |
| 4 |
| 1 |
| 2 |
∴AP=
| AC2+PC2 |
(
|
| 5 |
| 4 |
又∵OP=
| 1 |
| 2 |
∴当O、P、A三点共线时,A到原点O的距离最大.最大距离为OP+PA=1+
| 5 |
| 4 |
| 9 |
| 4 |

过A作AH⊥y轴,与BC的延长线交于点D,
∵AD∥OB,∴△POB∽△PAD,结合PB=OP得PD=AP=
| 5 |
| 4 |
由此可得DC=PD-CP=
| 5 |
| 4 |
| 1 |
| 4 |
又∵Rt△ACD∽Rt△OHA,AC=
| 3 |
| 4 |
∴
| AH |
| OH |
| DC |
| AC |
| 1 |
| 3 |
∵OA=
| 9 |
| 4 |
又∵Rt△OHA中,OA=
| OH2+AH2 |
| 9 |
| 4 |
∴AH=
| 9 |
| 40 |
| 10 |
| 27 |
| 40 |
| 10 |
| 9 |
| 40 |
| 10 |
| 27 |
| 40 |
| 10 |
点评:本题给出直角三角形在坐标系内滑动的模型,求滑动的过程中A到原点O的最大距离以及此时点A的坐标.着重考查了直线的基本量与基本形式、勾股定理与相似三角形、弧长公式与动点轨迹的求法等知识,属于中档题.

练习册系列答案
相关题目
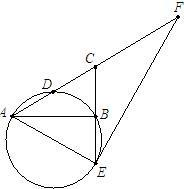 已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.
已知:如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,CB的延长线交过A、B、D三点的圆于点E.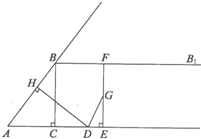 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.