摘要：解得 m>-1.∵ 当m>-1时.Δ>0.
网址：http://m.1010jiajiao.com/timu_id_6259[举报]
已知关于x的方程a2x2+（2a－1）x+1=0有两个实数根x1，x2．（1）当a为何值时，x1≠x2；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
解：（1）根据题意，得△=（2a－1）2－4a2>0，解得a<
．
∴当a<时，方程有两个不相等的实数根．
（2）存在，如果方程的两个实数根x1，x2互为相反数，则x1+x2=－
=0①，
解得a=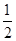
，经检验，a=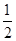是方程①的根．
∴当a=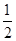时，方程的两个实数根x1与x2互为相反数．
上述解答过程是否有错误？如果有，请指出错误之处，并解答．
查看习题详情和答案>>
已知关于x的方程a2x2+（2a－1）x+1=0有两个实数根x1，x2．（1）当a为何值时，x1≠x2；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
解：（1）根据题意，得△=（2a－1）2－4a2>0，解得a<
．
∴当a<时，方程有两个不相等的实数根．
（2）存在，如果方程的两个实数根x1，x2互为相反数，则x1+x2=－
=0①，
解得a=
，经检验，a=是方程①的根．
∴当a=时，方程的两个实数根x1与x2互为相反数．
上述解答过程是否有错误？如果有，请指出错误之处，并解答．
4、解方程（x-1）2-5（x-1）+4=0时，我们可以将x-1看成一个整体，设x-1=y，则原方程可化为y2-5y+4=0，解得y1=1，y2=4．当y=1时，即x-1=1，解得x=2；当y=4时，即x-1=4，解得x=5，所以原方程的解为：x1=2，x2=5．则利用这种方法求得方程 （2x+5）2-4（2x+5）+3=0的解为（ ）
查看习题详情和答案>>