题目内容
阅读下列文字,然后解答问题解方程:x4-x2-6=0
解:设y=x2,则原方程可化为y2-y-6=0
解得 y1=3,y2=-2
当y=3时,x2=3解得x=±
| 3 |
∴原方程的解为x1=
| 3 |
| 3 |
观察上述解方程的过程,然后解方程:x4-5x2+6=0.
分析:设y=x2,则原方程可化为y2-5y+6=0,然后利用因式分解法解一元二次方程得到y1=3,y2=2,然后把y1=3,y2=2分别代入y=x2,再解一元二次方程即可.
解答:解:设y=x2,则原方程可化为y2-5y+6=0
解得 y1=3,y2=2
当y=3时,x2=3解得x=±
,当y=2时,x2=2解得x=±
,
∴原方程的解为x1=
,x2=-
,x3=
,x4=-
.
解得 y1=3,y2=2
当y=3时,x2=3解得x=±
| 3 |
| 2 |
∴原方程的解为x1=
| 3 |
| 3 |
| 2 |
| 2 |
点评:本题考查了利用换元法解高次方程:用一个字母表示高次方程中某一代数式,使高次方程转化为一元二次方程,然后把一元二次方程的解代入所设的等式中,再分别解两个一元二次方程得到原高次方程的解.也考查了利用因式分解法解一元二次方程.

练习册系列答案
相关题目
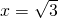 ,当y=-2时,x2=-2此方程无实数根,
,当y=-2时,x2=-2此方程无实数根,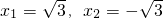
 ,当y=-2时,x2=-2此方程无实数根,
,当y=-2时,x2=-2此方程无实数根,