摘要：有 0=-2k+1.得 .∴ .当P点坐标为时.可设过P.B两点直线的解析式为y=kx-1.有 0=-2k-1.得 .∴ ..D(0.6)时.同理可得y=-3x+9.或 y=3x-9.或 .或 .
网址：http://m.1010jiajiao.com/timu_id_6240[举报]
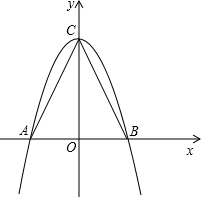（2012•柳州）如图，在△ABC中，AB=2，AC=BC=| 5 |
（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
| 1 |
| 2 |
（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，∴y1=1，y2=-1．
当x2=3，即y2=3，∴y3=
| 3 |
| 3 |
所以，原方程的解是y1=1，y2=-1，y3=
| 3 |
| 3 |
再如x2-2=4
| x2-2 |
| x2-2 |
（1）如图，有一个玩具火车放置在数轴上，若将火车在数轴上水平移动，则当A点移动到B点时，B点所对应的数为12；当B点移动到A点时，A点所对应的数为3（单位：单位长度）．由此可得玩具火车的长为
（2）现在你能用“数轴”这个工具解决下面问题吗？
一天，小明去问奶奶的年龄，奶奶说：“我若是你现在这么大，你还要40年才出生呢；你若是我现在这么大，我已是老寿星，116岁了！”小明心想：奶奶的年龄到底是多少岁呢？你能帮小明求出来吗？（可使用你喜欢的方法）
（3）在（1）的条件下数轴上放置与AB相同的玩具火车CD，使O与C重合，两列玩具火车分别从O和A同时出发向右移动，已知CD火车速度0.5个单位/秒，AB火车速度为1个单位/秒（两火车都可前后开动），问几秒后两火车头A与C相距10个单位？
查看习题详情和答案>>
3
3
个单位长度．（2）现在你能用“数轴”这个工具解决下面问题吗？
一天，小明去问奶奶的年龄，奶奶说：“我若是你现在这么大，你还要40年才出生呢；你若是我现在这么大，我已是老寿星，116岁了！”小明心想：奶奶的年龄到底是多少岁呢？你能帮小明求出来吗？（可使用你喜欢的方法）
（3）在（1）的条件下数轴上放置与AB相同的玩具火车CD，使O与C重合，两列玩具火车分别从O和A同时出发向右移动，已知CD火车速度0.5个单位/秒，AB火车速度为1个单位/秒（两火车都可前后开动），问几秒后两火车头A与C相距10个单位？
（2012•赤峰）阅读材料：
（1）对于任意两个数a、b的大小比较，有下面的方法：
当a-b＞0时，一定有a＞b；
当a-b=0时，一定有a=b；
当a-b＜0时，一定有a＜b．
反过来也成立．因此，我们把这种比较两个数大小的方法叫做“求差法”．
（2）对于比较两个正数a、b的大小时，我们还可以用它们的平方进行比较：
∵a2-b2=（a+b）（a-b），a+b＞0
∴（a2-b2）与（a-b）的符号相同
当a2-b2＞0时，a-b＞0，得a＞b
当a2-b2=0时，a-b=0，得a=b
当a2-b2＜0时，a-b＜0，得a＜b
解决下列实际问题：
（1）课堂上，老师让同学们制作几种几何体，张丽同学用了3张A4纸，7张B5纸；李明同学用了2张A4纸，8张B5纸．设每张A4纸的面积为x，每张B5纸的面积为y，且x＞y，张丽同学的用纸总面积为W1，李明同学的用纸总面积为W2．回答下列问题：
①W1=
W2=
②请你分析谁用的纸面积最大．
（2）如图1所示，要在燃气管道l上修建一个泵站，分别向A、B两镇供气，已知A、B到l的距离分别是3km、4km（即AC=3km，BE=4km），AB=xkm，现设计两种方案：
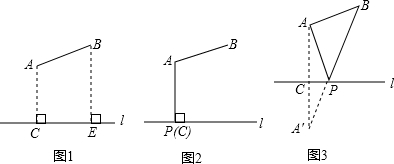
方案一：如图2所示，AP⊥l于点P，泵站修建在点P处，该方案中管道长度a1=AB+AP．
方案二：如图3所示，点A′与点A关于l对称，A′B与l相交于点P，泵站修建在点P处，该方案中管道长度a2=AP+BP．
①在方案一中，a1=
②在方案二中，a2=
km（用含x的式子表示）；
③请你分析要使铺设的输气管道较短，应选择方案一还是方案二．
查看习题详情和答案>>
（1）对于任意两个数a、b的大小比较，有下面的方法：
当a-b＞0时，一定有a＞b；
当a-b=0时，一定有a=b；
当a-b＜0时，一定有a＜b．
反过来也成立．因此，我们把这种比较两个数大小的方法叫做“求差法”．
（2）对于比较两个正数a、b的大小时，我们还可以用它们的平方进行比较：
∵a2-b2=（a+b）（a-b），a+b＞0
∴（a2-b2）与（a-b）的符号相同
当a2-b2＞0时，a-b＞0，得a＞b
当a2-b2=0时，a-b=0，得a=b
当a2-b2＜0时，a-b＜0，得a＜b
解决下列实际问题：
（1）课堂上，老师让同学们制作几种几何体，张丽同学用了3张A4纸，7张B5纸；李明同学用了2张A4纸，8张B5纸．设每张A4纸的面积为x，每张B5纸的面积为y，且x＞y，张丽同学的用纸总面积为W1，李明同学的用纸总面积为W2．回答下列问题：
①W1=
3x+7y
3x+7y
（用x、y的式子表示）W2=
2x+8y
2x+8y
（用x、y的式子表示）②请你分析谁用的纸面积最大．
（2）如图1所示，要在燃气管道l上修建一个泵站，分别向A、B两镇供气，已知A、B到l的距离分别是3km、4km（即AC=3km，BE=4km），AB=xkm，现设计两种方案：
方案一：如图2所示，AP⊥l于点P，泵站修建在点P处，该方案中管道长度a1=AB+AP．
方案二：如图3所示，点A′与点A关于l对称，A′B与l相交于点P，泵站修建在点P处，该方案中管道长度a2=AP+BP．
①在方案一中，a1=
（3+x）
（3+x）
km（用含x的式子表示）；②在方案二中，a2=
| x2+48 |
| x2+48 |
③请你分析要使铺设的输气管道较短，应选择方案一还是方案二．
