题目内容
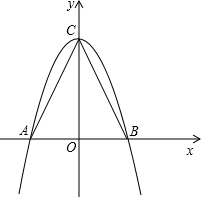 (2012•柳州)如图,在△ABC中,AB=2,AC=BC=
(2012•柳州)如图,在△ABC中,AB=2,AC=BC=| 5 |
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD=
| 1 |
| 2 |
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4-4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2-4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=-1.
当x2=3,即y2=3,∴y3=
| 3 |
| 3 |
所以,原方程的解是y1=1,y2=-1,y3=
| 3 |
| 3 |
再如x2-2=4
| x2-2 |
| x2-2 |
分析:(1)根据y轴是AB的垂直平分线,则可以求得OA,OB的长度,在直角△OBC中,利用勾股定理求得OC的长度,则A、B、C的坐标即可求解;
(2)利用待定系数法即可求得二次函数的解析式;
(3)首先求得△ABC的面积,根据S△ABD=
S△ABC,以及三角形的面积公式,即可求得D的纵坐标,把D的纵坐标代入二次函数的解析式,即可求得横坐标.
(4)设抛物线向右平移c个单位长度,则0<c≤1,可以写出平移以后的函数解析式,当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′•OB′,据此即可得到一个关于c的方程求得c的值.
(2)利用待定系数法即可求得二次函数的解析式;
(3)首先求得△ABC的面积,根据S△ABD=
| 1 |
| 2 |
(4)设抛物线向右平移c个单位长度,则0<c≤1,可以写出平移以后的函数解析式,当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′•OB′,据此即可得到一个关于c的方程求得c的值.
解答:解:(1)∵AB的垂直平分线为y轴,
∴OA=OB=
AB=
×2=1,
∴A的坐标是(-1,0),B的坐标是(1,0).
在直角△OBC中,OC=
=2,
则C的坐标是:(0,2);
(2)设抛物线的解析式是:y=ax2+b,
根据题意得:
,
解得:
,
则抛物线的解析式是:y=-2x2+2;
(3)∵S△ABC=
AB•OC=
×2×2=2,
∴S△ABD=
S△ABC=1.
设D的纵坐标是m,则
AB•|m|=1,
则m=±1.
当m=1时,-2x2+2=1,解得:x=±
,
当m=-1时,-2x2+2=-1,解得:x=±
,
则D的坐标是:(
,1)或(-
,1)或(
,-1),或(-
,-1).
(4)设抛物线向右平移c个单位长度,则0<c≤1,OA′=1-c,OB′=1+c.
平移以后的抛物线的解析式是:y=-2(x-c)2+b.
令x=0,解得y=-2c2+2.即OC′=-2c2+2.
当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′•OB′,
则(-2c2+2)2=(1-c)(1+c),
即(4c2-3)(c2-1)=0,
解得:c=
,-
(舍去),1,-1(舍去).
故平移
或1个单位长度.
∴OA=OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴A的坐标是(-1,0),B的坐标是(1,0).
在直角△OBC中,OC=
| BC2-OB2 |
则C的坐标是:(0,2);
(2)设抛物线的解析式是:y=ax2+b,
根据题意得:
|
解得:
|
则抛物线的解析式是:y=-2x2+2;
(3)∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABD=
| 1 |
| 2 |
设D的纵坐标是m,则
| 1 |
| 2 |
则m=±1.
当m=1时,-2x2+2=1,解得:x=±
| ||
| 2 |
当m=-1时,-2x2+2=-1,解得:x=±
| ||
| 2 |
则D的坐标是:(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(4)设抛物线向右平移c个单位长度,则0<c≤1,OA′=1-c,OB′=1+c.
平移以后的抛物线的解析式是:y=-2(x-c)2+b.
令x=0,解得y=-2c2+2.即OC′=-2c2+2.
当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′•OB′,
则(-2c2+2)2=(1-c)(1+c),
即(4c2-3)(c2-1)=0,
解得:c=
| ||
| 2 |
| ||
| 2 |
故平移
| ||
| 2 |
点评:本题考查了勾股定理,待定系数法求二次函数的解析式,以及图象的平移,正确理解:当点C′同时在以A′B′为直径的圆上时有:OC′2=OA•OB,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•柳州)如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,则∠DBC=
(2012•柳州)如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,则∠DBC= (2012•柳州)如图,AB是⊙O的直径,AC是弦.
(2012•柳州)如图,AB是⊙O的直径,AC是弦. (2012•柳州)如图,P1、P2、P3这三个点中,在第二象限内的有( )
(2012•柳州)如图,P1、P2、P3这三个点中,在第二象限内的有( ) (2012•柳州)如图,x和5分别是天平上两边的砝码,请你用大于号“>”或小于号“<”填空:x
(2012•柳州)如图,x和5分别是天平上两边的砝码,请你用大于号“>”或小于号“<”填空:x (2012•柳州)如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是一个特殊的四边形.
(2012•柳州)如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是一个特殊的四边形.