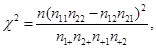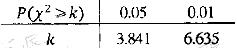网址:http://m.1010jiajiao.com/timu_id_574739[举报]
为了解某班学生喜爱打羽毛球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
|
|
|
50 |
已知在全部50人中随机抽取1人抽到不喜爱打羽毛球的学生的概率
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打羽毛球与性别有关?说明你的理由;
(3)已知喜爱打羽毛球的10位女生中, 还喜欢打篮球,
还喜欢打篮球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生
还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生 和
和 不全被选中的概率.下面的临界值表供参考:
不全被选中的概率.下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: 其中
其中 .)
.)
【解析】第一问利用数据写出列联表
第二问利用公式 计算的得到结论。
计算的得到结论。
第三问中,从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
 ,
,
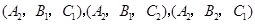 ,
,
基本事件的总数为8
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得
解:(1) 列联表补充如下:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
20 |
5 |
25 |
|
女生 |
10 |
15 |
25 |
|
合计 |
30 |
20 |
50 |
(2)∵
∴有99.5%的把握认为喜爱打篮球与性别有关
(3)从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
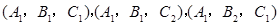 ,
,
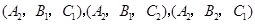 ,
,
基本事件的总数为8,
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得 .
.
查看习题详情和答案>>
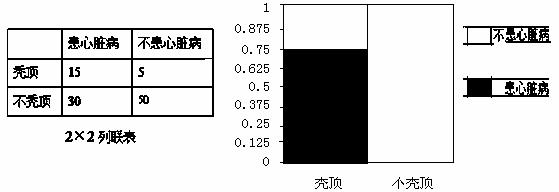
为了了解秃顶与患心脏病是否有关,某校学生随机调查了医院中因患心脏病而住院45名男性病人;另外不是因患心脏病而住院55名男性病人,得到相应的2×2列联表如下图:
(1)根据2×2列联表补全相应的等高条形图(用阴影表示);(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为秃顶与患心脏病有关?
(08年十校联考) (14分) 已知二次函数![]() 同时满足:⑴不等式
同时满足:⑴不等式![]() 的解集有且只有一个元素;⑵在定义域内存在
的解集有且只有一个元素;⑵在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立。设数列
成立。设数列![]() 的前
的前![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]()
(3)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 这个数列
这个数列![]() 的变号数。另
的变号数。另![]()


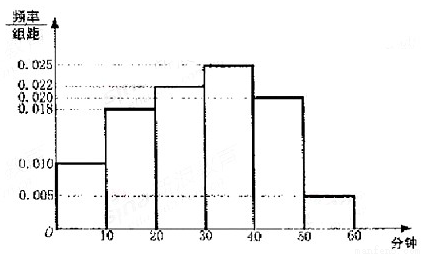
 列联表,并据此资料你是否认为“体育迷”与性别
列联表,并据此资料你是否认为“体育迷”与性别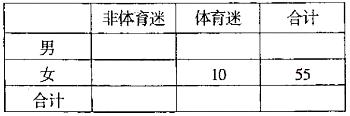
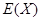 和方差
和方差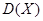 。
。