摘要：当且仅当t=2时.△AOP的面积的最小值为2.??????????????????????????????12分
网址：http://m.1010jiajiao.com/timu_id_574648[举报]
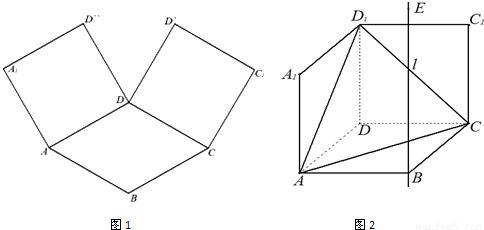
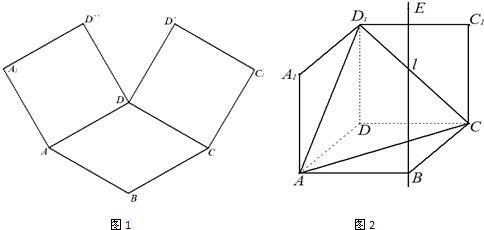
如图1，在平面内，ABCD边长为2的正方形，ADD″A1和CDD″C1都是正方形．将两个正方形分别沿AD，CD折起，使D″与D′重合于点D1．设直线l过点B且垂直于正方形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧，设BE=t（t＞0）（图2）．
（1）设二面角E-AC-D1的大小为θ，当t=2时，求θ的余弦值；
（2）当t＞2时在线段D1E上是否存在点P，使平面PA1C1∥平面EAC，若存在，求出P分
所成的比λ；若不存在，请说明理由．
查看习题详情和答案>>
（1）设二面角E-AC-D1的大小为θ，当t=2时，求θ的余弦值；
（2）当t＞2时在线段D1E上是否存在点P，使平面PA1C1∥平面EAC，若存在，求出P分
| D1E |
查看习题详情和答案>>
下列命题成立的是
①a，bc∈R，a2+b2+c2≥ab+bc+ac；
②当x＞0时，函数f(x)=
+2x≥2
=2
，∴当且仅当x2=2x即x=2时f（x）取最小值；
③当x＞1时，
≥5；
④当x＞0时，x+
+
的最小值为
．
查看习题详情和答案>>
①③④
①③④
． （写出所有正确命题的序号）．①a，bc∈R，a2+b2+c2≥ab+bc+ac；
②当x＞0时，函数f(x)=
| 1 |
| x2 |
|
|
③当x＞1时，
| x2-x+4 |
| x-1 |
④当x＞0时，x+
| 1 |
| x |
| 1 | ||
x+
|
| 5 |
| 2 |
已知在数列{an}中，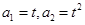
（t>0且t≠1）．
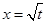是函数
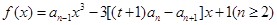的一个极值点．
（1）证明数列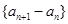
是等比数列，并求数列
的通项公式；
（2）记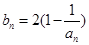
，当t=2时，数列
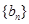的前n项和为Sn，求使Sn>2012的n的最小值；
（3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有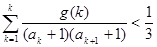
成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．
查看习题详情和答案>>
（t>0且t≠1）．若
是函数
的一个极值点．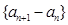
是等比数列，并求数列
的通项公式；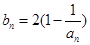
，当t=2时，数列
的前n项和为Sn，求使Sn>2008的n的最小值；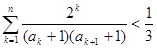
。
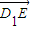所成的比λ；若不存在，请说明理由．