网址:http://m.1010jiajiao.com/timu_id_574446[举报]
一、选择题:本大题共12小题,每小题5分,共60分.
BCBBA BCDCB DA
二.填空题:本大题共4小题,每小题5分,共20分.
13. 2 14 .
14 .  15.
4 16.
15.
4 16. 
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17. (本大题共10分)
解: 4分
4分
或 8分
8分
故原不等式的解集为 10分
10分
18. (本小题满分12分)
解:(1) ,
, ,且
,且 .
.
 ,即
,即 ,又
,又 ,
, ……..2分
……..2分
又由 ,
, 5分
5分
(2)由正弦定理得: ,
7分
,
7分
又 ,
,
 …………9分
…………9分
 ,则
,则 .则
.则 ,
,
即 的取值范围是
的取值范围是 …………………
12分
…………………
12分
19.(本小题满分12分)
(1)解:设“射手射击1次,击中目标”为事件A
则在3次射击中至少有两次连续击中目标的概率

 =
= 7分
7分
(2)解:射手第3次击中目标时,恰好射击了4次的概率
 12分
12分
20. (本小题满分12分)
(Ⅰ)∵
∴ 2分
2分
∵ 4分
4分
∴ 6分
6分
(Ⅱ)∵函数 在区间
在区间 上单调递增
上单调递增
∴ 对一切
对一切 恒成立
恒成立
方法1  时成立
时成立
当 时,等价于不等式
时,等价于不等式 恒成立
恒成立
令
当 时取到等号,所以
时取到等号,所以
∴ 12分
12分
方法2 设
对称轴
当 时,要满足条件,只要
时,要满足条件,只要 成立
成立
当 时,
时, ,∴
,∴
当 时,只要
时,只要 矛盾
矛盾
综合得 12分
12分
21.(本小题满分12分)
解:(Ⅰ)设 的公差为d,{Bn}的公比为q,则依题意有q>0且
的公差为d,{Bn}的公比为q,则依题意有q>0且

解得d=2,q=2.
所以,  ,
,
 6分
6分
(Ⅱ) 错位相减法得:
错位相减法得: n=1,2,3…
12分
n=1,2,3…
12分
22.(本小题满分12分)
解:(I)由

故 的方程为
的方程为 点A的坐标为(1,0)
2分
点A的坐标为(1,0)
2分
设
由
整理 4分
4分
 M的轨迹C为以原点为中心,焦点在x轴上,长轴长为
M的轨迹C为以原点为中心,焦点在x轴上,长轴长为 ,短轴长为2的椭圆 5分
,短轴长为2的椭圆 5分
(II)如图,由题意知 的斜率存在且不为零,
的斜率存在且不为零,
设 方程为
方程为 ①
①
将①代入 ,整理,得
,整理,得
 7分
7分
设 、
、 ,则
,则 ②
②
令 由此可得
由此可得
由②知

 ,
,
即 10分
10分


解得
又
 面积之比的取值范围是
面积之比的取值范围是 12分
12分
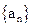 的通项公式为
的通项公式为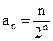 ,则前
,则前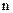 项和为( )
项和为( )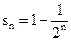 B
B 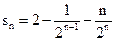 C
C 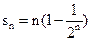 D
D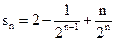
 的通项公式为
的通项公式为 ,其前
,其前 项和为
项和为 ,则
,则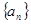 的通项公式为
的通项公式为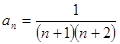 ,其前
,其前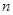 项和为
项和为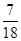 ,则
,则 的通项公式为
的通项公式为 ,其前
,其前 项和为
项和为 ,则
,则 的通项公式为
的通项公式为 ,其前
,其前 项和为
项和为 ,则
,则