网址：http://m.1010jiajiao.com/timu_id_573896[举报]
一、选择题（本题共10小题，每小题4分，共40分，有的小题只有一个选项符合题意，有的小题有几个选项符合题意，全部选对得4分，部分选对得2分，选错或不答得0分）
题号
1
2
3
4
5
6
7
8
9
10
答案
ABD
C
C
C
BD
C
AD
D
A
AB
二、实验题（每小题4分，共12分）
11、(1) B (2) ACD (3) AEG
三、计算题（共4小题，每小题12分，共48分.解答应写出必要的文字说明，方程式和重要的演算步骤，只写出最后答案的不能得分。有数值计算的题，答案必须写出数值和单位）
12．解：(1)对A、B整体：3qE－qE＝2ma ① 得：a＝qE/m ②
(2)设所求的距离为L，则对B有：
③
②、③联立得；
13．解：碰撞过程动量守恒mvo=(m+M)V ①
由能量守恒得 FS=
②
设木板的长度为L，应满足：L≥S ③
由动量定理：Ft=MV ④
由①②③联立得：
由①②④联立得：
14．解：前10s做匀加速运动F－μmgㄔma
且a=
后4s做匀减速运动F/3 ―μmg=ma’ 且a’=－
联解得：μ=
15．解：碰撞过程，动量守恒：m1V1=
m1V1/+ m2V2 所以：V1/＝－
碰撞后m2上滑过程机械能守恒，设最大偏角为θ，则：
Cosθ=0.997 所以：θ=4.4°＜10°
因此：m2在圆弧上的运动当作简谐振动处理，故：t1=
t2=S/ V2=1.2/0.6=2s t3=S/ V1/ =1.2/0.3=4s
因为两物体平抛运动的时间相同，所以，所求的时间差为：△t＝t1+ t2－t3＝0.43s
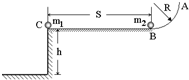如图，AB为半径R=6m的1/4光滑圆弧形，导轨圆心与A点等高．BC为长S=1.2m的光滑水平导轨，在B点与圆弧导轨相切，离地面高度h=2m．一质量m1=0.2kg的小球置于C点，另一质量为m2=0.4kg的小球置于B点，现给小球m1以V1=0.9m/s的水平速度，当m1运动到B时与m2发生正碰，碰后m2获得V2=0.6m/s的速度，g=10m/s2，求从碰撞后到两球落地的时间差．（arccos0.997=4.4°，| 0.6 |
（09年天水一中期末）（12分）如图，AB为半径R=6m的1/4光滑圆弧形，导轨圆心与A点等高。BC为长S=1.2m的光滑水平导轨，在B点与圆弧导轨相切，离地面高度h=2m。一质量m1=0.2kg的小球置于C点，另一质量为m2=0.4kg的小球置于B点，现给小球m1以V1=0.9m/s的水平速度，当m1运动到B时与m2发生正碰，碰后m2获得V2=0.6m/s的速度，g=10 m/s2，求从碰撞后到两球落地的时间差。(arccos0.997=4.4°，
,结果保留两位有效数字)
查看习题详情和答案>>
如图，传送带AB总长为l=10m，与一个半径为R=0.4m的光滑1/4圆轨道BC相切于B点。传送带速度恒为v=6m/s，方向向右。现有一个滑块以一定初速度v0从A点水平冲上传送带，滑块质量为m=10kg，滑块与传送带间的动摩擦因数为μ=0.1。已知滑块运动到B端时，刚好与传送带共速。
求
（1）v0；
（2）滑块能上升的最大高度h；
（3）求滑块第二次在传送带上滑行时，滑块和传送带系统产生的内能。
