题目内容
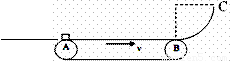
如图，传送带AB总长为l=10m，与一个半径为R=0.4m的光滑1/4圆轨道BC相切于B点。传送带速度恒为v=6m/s，方向向右。现有一个滑块以一定初速度v0从A点水平冲上传送带，滑块质量为m=10kg，滑块与传送带间的动摩擦因数为μ=0.1。已知滑块运动到B端时，刚好与传送带共速。
求
（1）v0；
（2）滑块能上升的最大高度h；
（3）求滑块第二次在传送带上滑行时，滑块和传送带系统产生的内能。
（1）v0=4m/s或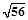
m/s （2）1.8m （3）220J
解析试题分析：（1）滑块运动过程中加速度为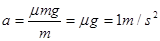
若物体的速度小于传送带的速度，加速度为正，则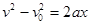
，解得
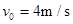
若物体的速度大于传送带的速度，加速度为负，则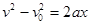，解得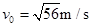
（2）上升过程中机械能守恒，则：
解得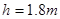
（3）滑块第二次在传送带上滑行时，假如滑块只做减速运动，加速度为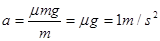，减速运动的位移为：
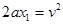，即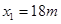
，所以滑块到A端时速度不为零，
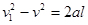，解得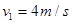
，故此过程中传送带的位移为
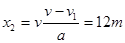，所以滑块和传送带的相对位移为
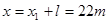，故摩擦力做功为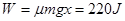
考点：考查了牛顿第二定律以及动能定理的应用
点评：在分析第一问时，一定要注意滑块在传送带上有可能做减速运动，即传送带的速度小于滑块的速度，
练习册系列答案
相关题目
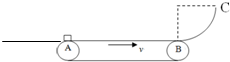如图，传送带AB总长为l=10m，与一个半径为R=0.4m的光滑
