摘要:24.(1)解:如图3.连结OB.-----------1分 ∵⊙O的内接△ABC中.∠BAC=45°.∴∠BOC=2∠BAC=90°.∵OB=OC.∴∠OBC=∠OCB=45°. ∵AD∥OC.∴∠D=∠OCB=45°.--------------------2分 (2)证明:∵∠BAC=45°.∠D=45°. ∴∠BAC=∠D.----------------------3分 ∵AD∥OC.西城区初三数学试卷答案及评分参考第4页 ∴∠ACE=∠DAC.------------------------4分∴△ACE∽△DAC.
网址:http://m.1010jiajiao.com/timu_id_570088[举报]
如图,OB、OC分别为∠ABC,∠ACB的平分线,∠BOC随着∠A的变化而变化.为探究∠A和∠BOC的关系,现采取如下两种方案,在变化过程中,设∠A为x°,∠BOC为y°.
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下: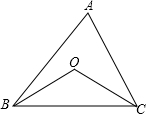
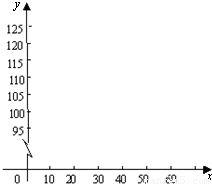
建立直角坐标系,并描点、连线,猜测y与x之间的函数关系,求出y与x的函数关系式.
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y= .(请直接写 出结果)
出结果)
(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系. 查看习题详情和答案>>
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下:

| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y=
 出结果)
出结果)(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系. 查看习题详情和答案>>
如图,OB、OC分别为∠ABC,∠ACB的平分线,∠BOC随着∠A的变化而变化.为探究∠A和∠BOC的关系,现采取如下两种方案,在变化过程中,设∠A为x°,∠BOC为y°.
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下: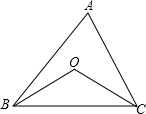
| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y=______.(请直接写
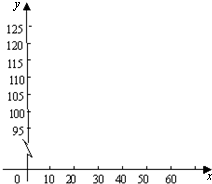 出结果)
出结果)(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系. 查看习题详情和答案>>
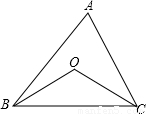
如图,OB、OC分别为∠ABC,∠ACB的平分线,∠BOC随着∠A的变化而变化.为探究∠A和∠BOC的关系,现采取如下两种方案,在变化过程中,设∠A为x°,∠BOC为y°.
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下:
建立直角坐标系,并描点、连线,猜测y与x之间的函数关系,求出y与x的函数关系式.
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y=______.(请直接写出结果)
(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系.
 查看习题详情和答案>>
查看习题详情和答案>>
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下:
| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y=______.(请直接写出结果)
(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系.

 查看习题详情和答案>>
查看习题详情和答案>>
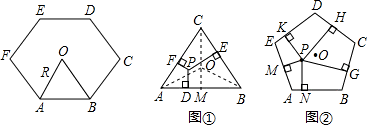 同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
探索发现:
(1)为了解决这个问题,我们不妨从最简单的正多边形--正三角形入手.
如图①,△ABC是正三角形,半径OA=R,∠AOB是中心角,P是△ABC内任意一点,P到△ABC各边距离分别为h1、h2、h3 ,确定h1+h2+h3的值与△ABC的半径R及中心角的关系.
解:设△ABC的边长是a,面积为S,显然S= a(h1+h2+h3)
a(h1+h2+h3)
O为△ABC的中心,连接OA、OB、OC,它们将△ABC分成三个全等的等腰三角形,过点O作OM⊥AB,垂足为M,Rt△AOM中,易知
OM=OAcos∠AOM=Rcos ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°,
AM=OAsin∠AOM=Rsin ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60°
∴AB=a=2AM=2Rsin60°
∴S△AOB= AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60°
∴S△ABC=3S△AOB=3R2sin60°cos60°
∴ a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60°
即: ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
∴h1+h2+h3=3Rcos60°
(2)如图②,五边形ABCDE是正五边形,半径是R,P是正五边形ABCDE内任意一点,P到五边形ABCDE各边距离分别为h1、h2、h3、h4、h5,参照(1)的探索过程,确定h1+h2+h3+h4+h5的值与正五边形ABCDE的半径R及中心角的关系.
(3)类比上述探索过程,直接填写结论
正六边形(半径是R)内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6=________
正八边形(半径是R)内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6+h7+h8=________
正n边形(半径是R)内任意一点P到各边距离之和 h1+h2+…+hn=________.
查看习题详情和答案>>
同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
探索发现:
(1)为了解决这个问题,我们不妨从最简单的正多边形--正三角形入手.
如图①,△ABC是正三角形,半径OA=R,∠AOB是中心角,P是△ABC内任意一点,P到△ABC各边距离分别为h1、h2、h3 ,确定h1+h2+h3的值与△ABC的半径R及中心角的关系.
解:设△ABC的边长是a,面积为S,显然S= a(h1+h2+h3)
a(h1+h2+h3)
O为△ABC的中心,连接OA、OB、OC,它们将△ABC分成三个全等的等腰三角形,过点O作OM⊥AB,垂足为M,Rt△AOM中,易知
OM=OAcos∠AOM=Rcos ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°,
AM=OAsin∠AOM=Rsin ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60°
∴AB=a=2AM=2Rsin60°
∴S△AOB= AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60°
∴S△ABC=3S△AOB=3R2sin60°cos60°
∴ a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60°
即: ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
∴h1+h2+h3=3Rcos60°
(2)如图②,五边形ABCDE是正五边形,半径是R,P是正五边形ABCDE内任意一点,P到五边形ABCDE各边距离分别为h1、h2、h3、h4、h5,参照(1)的探索过程,确定h1+h2+h3+h4+h5的值与正五边形ABCDE的半径R及中心角的关系.
(3)类比上述探索过程,直接填写结论
正六边形(半径是R)内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6=______
正八边形(半径是R)内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6+h7+h8=______
正n边形(半径是R)内任意一点P到各边距离之和 h1+h2+…+hn=______.
 查看习题详情和答案>>
查看习题详情和答案>>
探索发现:
(1)为了解决这个问题,我们不妨从最简单的正多边形--正三角形入手.
如图①,△ABC是正三角形,半径OA=R,∠AOB是中心角,P是△ABC内任意一点,P到△ABC各边距离分别为h1、h2、h3 ,确定h1+h2+h3的值与△ABC的半径R及中心角的关系.
解:设△ABC的边长是a,面积为S,显然S=
 a(h1+h2+h3)
a(h1+h2+h3)O为△ABC的中心,连接OA、OB、OC,它们将△ABC分成三个全等的等腰三角形,过点O作OM⊥AB,垂足为M,Rt△AOM中,易知
OM=OAcos∠AOM=Rcos
 ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°,AM=OAsin∠AOM=Rsin
 ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60°∴AB=a=2AM=2Rsin60°
∴S△AOB=
 AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60°∴S△ABC=3S△AOB=3R2sin60°cos60°
∴
 a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60°即:
 ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°∴h1+h2+h3=3Rcos60°
(2)如图②,五边形ABCDE是正五边形,半径是R,P是正五边形ABCDE内任意一点,P到五边形ABCDE各边距离分别为h1、h2、h3、h4、h5,参照(1)的探索过程,确定h1+h2+h3+h4+h5的值与正五边形ABCDE的半径R及中心角的关系.
(3)类比上述探索过程,直接填写结论
正六边形(半径是R)内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6=______
正八边形(半径是R)内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6+h7+h8=______
正n边形(半径是R)内任意一点P到各边距离之和 h1+h2+…+hn=______.
 查看习题详情和答案>>
查看习题详情和答案>>