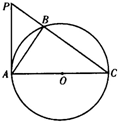
摘要:例2.OA是圆C的直径.OA=2a.射线OB与圆交于Q点.和经过A点的切线交于B点.作PQ⊥OA.PB∥OA.求点P的轨迹方程解:[方法一]设P(x,y)是轨迹上任意一点.取∠DOQ=θ.由已知x=OD=OQ.cosθ=OA.cosθ=2acos2θ.y=AB=OA.tanθ=2a.tan2θ,故P点的参数方程为
网址:http://m.1010jiajiao.com/timu_id_569757[举报]
已知点A(x1,y1),B(x2,y2)(x1x2≠0)是抛物线y2=2px(p>0)上的两个动点,O是坐标原点,向量
,
满足|
+
|=|
-
|,设圆C的方程为x2+y2-(x1+x2)x-(y1+y2)y=0.
(1)证明线段AB是圆C的直径;
(2)当圆C的圆心到直线x-2y=0的距离的最小值为
时,求p的值.
查看习题详情和答案>>
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
(1)证明线段AB是圆C的直径;
(2)当圆C的圆心到直线x-2y=0的距离的最小值为
2
| ||
| 5 |
已知点A(x1,y1),B(x2,y2)(x1x2≠0)是抛物线y2=2px(p>0)上的两个动点,O是坐标原点,向量
,
满足|
+
|=|
-
|,设圆C的方程为x2+y2-(x1+x2)x-(y1+y2)y=0.
(1)证明线段AB是圆C的直径;
(2)当圆C的圆心到直线x-2y=0的距离的最小值为
时,求p的值.
查看习题详情和答案>>
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
(1)证明线段AB是圆C的直径;
(2)当圆C的圆心到直线x-2y=0的距离的最小值为
2
| ||
| 5 |
已知圆C经过A(0,1),B(4,a)(a∈R)两点.
(1)当a=3,并且AB是圆C的直径,求此时圆C的标准方程;
(2)当a=1时,圆C与x轴相切,求此时圆C的方程;
(3)如果AB是圆C的直径,证明:无论a取何实数,圆C恒经过除A外的另一个定点,求出这个定点坐标.
查看习题详情和答案>>
(1)当a=3,并且AB是圆C的直径,求此时圆C的标准方程;
(2)当a=1时,圆C与x轴相切,求此时圆C的方程;
(3)如果AB是圆C的直径,证明:无论a取何实数,圆C恒经过除A外的另一个定点,求出这个定点坐标.
 (二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)
(二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)