题目内容
 (二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)
(二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)A.(不等式选讲) 函数f(x)=
| |x-2|-1 |
(-∞,1]∪[3,+∞)
(-∞,1]∪[3,+∞)
B.(坐标系与参数方程)已知极点在直角坐标系的原点O处,极轴与x轴的正半轴重合,曲线C的极坐标方程为ρ=2cosθ,直线l的参数方程为
|
| 2 |
| 5 |
| 2 |
| 5 |
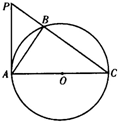
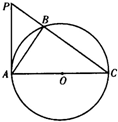
C.(几何证明选讲)如图,PA是圆O的切线,切点为A,PA=2.AC是圆O的直径,PC与圆O交于B,PB=1,则AC=
2
| 3 |
2
.| 3 |
分析:A,直接根据根号内有意义即可求出结论;
B,先分别求出其直角坐标系方程,再求出圆心到直线的距离即可得到答案;
C,直接根据切割线定理求出PC,再结合直角三角形即可求出答案.
B,先分别求出其直角坐标系方程,再求出圆心到直线的距离即可得到答案;
C,直接根据切割线定理求出PC,再结合直角三角形即可求出答案.
解答:解:A:因为:|x-2|-1≥0⇒|x-2|≥1⇒x≥3或x≤1.
即定义域为:(-∞,1]∪[3,+∞).
B:∵曲线C的极坐标方程为ρ=2cosθ,
∴
=2•
⇒x2+y2=2x⇒(x-1)2+y2=1.即是圆心为(1,0),半径为1的圆.
直线l的参数方程为
(t为参数)⇒y=1+
x⇒4x-3y+3=0.
所以圆心到直线的距离d=
=
.
故曲线C上的点到直线l的最短距离为:
-r=
.
C:∵PA是圆O的切线,切点为A,PA=2.AC是圆O的直径,PC与圆O交于B,PB=1
∴PA2=PB•PC⇒PC=4.
∴AC=
=
=2
.
故答案为:(-∞,1]∪[3,+∞),
,2
.
即定义域为:(-∞,1]∪[3,+∞).
B:∵曲线C的极坐标方程为ρ=2cosθ,
∴
| x2+y2 |
| x | ||
|
直线l的参数方程为
|
| 4 |
| 3 |
所以圆心到直线的距离d=
| |4×1-3×0+3| | ||
|
| 7 |
| 5 |
故曲线C上的点到直线l的最短距离为:
| 7 |
| 5 |
| 2 |
| 5 |
C:∵PA是圆O的切线,切点为A,PA=2.AC是圆O的直径,PC与圆O交于B,PB=1
∴PA2=PB•PC⇒PC=4.
∴AC=
| PC2-PA2 |
| 42-22 |
| 3 |
故答案为:(-∞,1]∪[3,+∞),
| 2 |
| 5 |
| 3 |
点评:本题主要考察简单曲线的极坐标方程以及与圆有关的比例线段,和绝对值不等式的解法.一般这种题目考察的都比较基础,属于基础题目.

练习册系列答案
相关题目
 (二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)
(二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)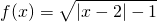 的定义域为________
的定义域为________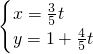 (t为参数).则曲线C上的点到直线l的最短距离为________.
(t为参数).则曲线C上的点到直线l的最短距离为________. 的定义域为
的定义域为  (t为参数).则曲线C上的点到直线l的最短距离为 .
(t为参数).则曲线C上的点到直线l的最短距离为 .