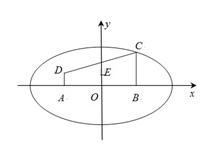
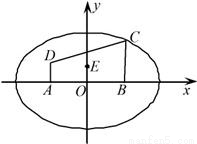
摘要：椭圆标准方程的推导如图.建立直角坐标系xOy.使x轴经过点F1.F2.并且O与线段F1F2的中点重合.设M(x,y)是椭圆上任意一点.椭圆的焦距为2c(c＞0).那么焦点F1.F2的坐标分别是(-c,0).(c,0).又设M与F1和F2的距离的和等于常数2a.由椭圆定义.椭圆就是集合P={MㄏMF1+MF2=2a}
网址：http://m.1010jiajiao.com/timu_id_567516[举报]
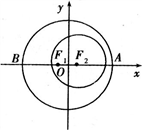
我国发射的第一颗人造地球卫星的运行轨道，是以地心（地球的中心）F2为一个焦点的椭圆，已知它的近地点A（离地面最近的点）距地面439 km，远地点B(离地面最远的点)距地面2 384 km，并且F2、A、B在同一直线上，地球半径约为6 371 km，求卫星运行的轨道方程（精确到1 km）．如图，建立直角坐标系，使点A，B，F2在x轴上，F2为椭圆右焦点（记F1为左焦点）
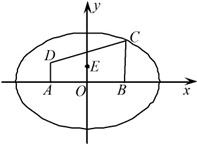
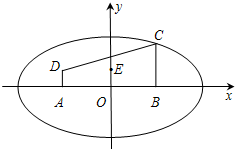如图，在直角坐标系xOy中有一直角梯形ABCD，AB的中点为O，AD⊥AB，AD∥BC，AB=4，BC=3，AD=1，以A，B为焦点的椭圆经过点C．（1）求椭圆的标准方程；
（2）若点E（0，1），问是否存在直线l与椭圆交于M，N两点且|ME|=|NE|，若存在，求出直线l的斜率的取值范围；若不存在，请说明理由．
中有一直角梯形
，
的中点为
，
，
，
，
，
，以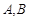
为焦点的椭圆经过点
.
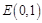，问是否存在直线
与椭圆交于
两点且
，若存在，求出直线
