摘要：学习了椭圆的定义.也有类似的思考 二.建构数学
网址：http://m.1010jiajiao.com/timu_id_567515[举报]
已知抛物线y2=2px（p＞0），椭圆| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
（1）在抛物线中，已知∠AKB为直角，则在椭圆和双曲线中∠AKB还为直角吗？试证明你的合情推理所得到的结论；
（2）在抛物线中，已知直线KA与抛物线只有一个公共点A，则在椭圆和双曲线中也有类似的性质吗？试选择椭圆证明你的类比推理．
已知抛物线y2=2px（p＞0），椭圆
，双曲线
，如图示，K为与焦点F对应的准线与x轴的交点，AB为过焦点的垂直于x轴的弦．
（1）在抛物线中，已知∠AKB为直角，则在椭圆和双曲线中∠AKB还为直角吗？试证明你的合情推理所得到的结论；
（2）在抛物线中，已知直线KA与抛物线只有一个公共点A，则在椭圆和双曲线中也有类似的性质吗？试选择椭圆证明你的类比推理．
查看习题详情和答案>>
，双曲线，如图示，K为与焦点F对应的准线与x轴的交点，AB为过焦点的垂直于x轴的弦．（1）在抛物线中，已知∠AKB为直角，则在椭圆和双曲线中∠AKB还为直角吗？试证明你的合情推理所得到的结论；
（2）在抛物线中，已知直线KA与抛物线只有一个公共点A，则在椭圆和双曲线中也有类似的性质吗？试选择椭圆证明你的类比推理．
查看习题详情和答案>>
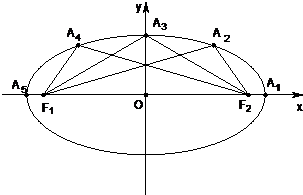（文科做）已知点A1（2，0），A2（1，t），A3（0，b），A4（-1，t），A5（-2，0），其中t＞0，b为正常数．（1）半径为2的圆C1经过Ai（i=1，2，…，5）这五个点，求b和t的值；
（2）椭圆C2以F1（-c，0），F2（c，0）（c＞0）为焦点，长轴长是4．若AiF1+AiF2=4（i=1，2，…，5），试用b表示t；
（3）在（2）中的椭圆C2中，两线段长的差A1F1-A1F2，A2F1-A2F2，…，A5F1-A5F2构成一个数列{an}，求证：对n=1，2，3，4都有an+1＜an．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）
（文科做）已知点A1（2，0），A2（1，t），A3（0，b），A4（-1，t），A5（-2，0），其中t＞0，b为正常数．
（1）半径为2的圆C1经过Ai（i=1，2，…，5）这五个点，求b和t的值；
（2）椭圆C2以F1（-c，0），F2（c，0）（c＞0）为焦点，长轴长是4．若AiF1+AiF2=4（i=1，2，…，5），试用b表示t；
（3）在（2）中的椭圆C2中，两线段长的差A1F1-A1F2，A2F1-A2F2，…，A5F1-A5F2构成一个数列{an}，求证：对n=1，2，3，4都有an+1＜an．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）
查看习题详情和答案>>
（文科做）已知点A1（2，0），A2（1，t），A3（0，b），A4（-1，t），A5（-2，0），其中t＞0，b为正常数．
（1）半径为2的圆C1经过Ai（i=1，2，…，5）这五个点，求b和t的值；
（2）椭圆C2以F1（-c，0），F2（c，0）（c＞0）为焦点，长轴长是4．若AiF1+AiF2=4（i=1，2，…，5），试用b表示t；
（3）在（2）中的椭圆C2中，两线段长的差A1F1-A1F2，A2F1-A2F2，…，A5F1-A5F2构成一个数列{an}，求证：对n=1，2，3，4都有an+1＜an．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）
查看习题详情和答案>>
（1）半径为2的圆C1经过Ai（i=1，2，…，5）这五个点，求b和t的值；
（2）椭圆C2以F1（-c，0），F2（c，0）（c＞0）为焦点，长轴长是4．若AiF1+AiF2=4（i=1，2，…，5），试用b表示t；
（3）在（2）中的椭圆C2中，两线段长的差A1F1-A1F2，A2F1-A2F2，…，A5F1-A5F2构成一个数列{an}，求证：对n=1，2，3，4都有an+1＜an．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）
查看习题详情和答案>>