题目内容
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.(1)半径为2的圆C1经过Ai(i=1,2,…,5)这五个点,求b和t的值;
(2)椭圆C2以F1(-c,0),F2(c,0)(c>0)为焦点,长轴长是4.若AiF1+AiF2=4(i=1,2,…,5),试用b表示t;
(3)在(2)中的椭圆C2中,两线段长的差A1F1-A1F2,A2F1-A2F2,…,A5F1-A5F2构成一个数列{an},求证:对n=1,2,3,4都有an+1<an.(本小题解答中用到了椭圆的第一定义与焦半径公式,新教材实验区的学生可不解第三小题,请学习时注意)

【答案】分析:(1)注意到A1(2,0),A5(-2,0),且半径为2的圆C1经过Ai,故线段A1A5就是所求圆的直径,O为圆心,写出圆的标准方程即可
(2)椭圆长轴长是4,即a=2,故可设椭圆方程为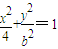 ,因为AiF1+AiF2=4,由椭圆定义知点A2(1,t)在椭圆上,代入椭圆方程即可用b表示t;
,因为AiF1+AiF2=4,由椭圆定义知点A2(1,t)在椭圆上,代入椭圆方程即可用b表示t;
(3)利用焦半径公式,AiF1=exi+a,再利用椭圆定义,即可得AiF1-AiF2=2AiF1-2a=2exi,可见数列{an}的项的大小只与点Ai的横坐标有关,进而易证an+1<an.
解答:解:(1)∵A1A5=4,则A1A5为⊙C1的直径,∴圆心为A1,A5的中点(0,0)
∴⊙C1的方程是x2+y2=4,
∵A2(1,t),A3(0,b)在圆上,
∴b=2,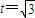 ;
;
(2)∵椭圆C2以F1(-c,0),F2(c,0)(c>0)为焦点,长轴长是4,
∴椭圆C2的方程是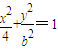 ,将A2(1,t)代入,
,将A2(1,t)代入,
得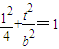 ,得
,得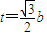 ;
;
(3)设Ai的坐标是(xi,yi),∵椭圆C2的左准线为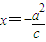 ,
,
∴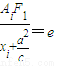 ,则
,则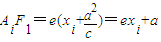 ,(其中
,(其中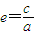 为椭圆的离心率)
为椭圆的离心率)
AiF1-AiF2=2AiF1-2a=2exi
由于{xi}递减,则对n=1,2,3,4都有an+1<an.
点评:本题考察了圆的标准方程,椭圆的标准方程,椭圆的定义,椭圆的几何性质等基础知识及其应用,本题解答中用到了椭圆的第二定义转化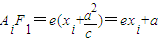 ,新教材实验区的学生可不解第三小题,请学习时注意
,新教材实验区的学生可不解第三小题,请学习时注意
(2)椭圆长轴长是4,即a=2,故可设椭圆方程为
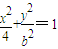 ,因为AiF1+AiF2=4,由椭圆定义知点A2(1,t)在椭圆上,代入椭圆方程即可用b表示t;
,因为AiF1+AiF2=4,由椭圆定义知点A2(1,t)在椭圆上,代入椭圆方程即可用b表示t;(3)利用焦半径公式,AiF1=exi+a,再利用椭圆定义,即可得AiF1-AiF2=2AiF1-2a=2exi,可见数列{an}的项的大小只与点Ai的横坐标有关,进而易证an+1<an.
解答:解:(1)∵A1A5=4,则A1A5为⊙C1的直径,∴圆心为A1,A5的中点(0,0)
∴⊙C1的方程是x2+y2=4,
∵A2(1,t),A3(0,b)在圆上,
∴b=2,
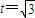 ;
; (2)∵椭圆C2以F1(-c,0),F2(c,0)(c>0)为焦点,长轴长是4,
∴椭圆C2的方程是
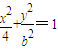 ,将A2(1,t)代入,
,将A2(1,t)代入,得
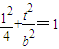 ,得
,得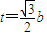 ;
; (3)设Ai的坐标是(xi,yi),∵椭圆C2的左准线为
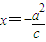 ,
,∴
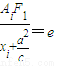 ,则
,则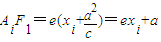 ,(其中
,(其中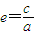 为椭圆的离心率)
为椭圆的离心率)AiF1-AiF2=2AiF1-2a=2exi
由于{xi}递减,则对n=1,2,3,4都有an+1<an.
点评:本题考察了圆的标准方程,椭圆的标准方程,椭圆的定义,椭圆的几何性质等基础知识及其应用,本题解答中用到了椭圆的第二定义转化
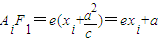 ,新教材实验区的学生可不解第三小题,请学习时注意
,新教材实验区的学生可不解第三小题,请学习时注意 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数. (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.