摘要: 已知:是上的奇函数.且满足.
网址:http://m.1010jiajiao.com/timu_id_564879[举报]
一、1. 2.3 3.
2.3 3. 4.18 5.
4.18 5. 6.55 7.
6.55 7. 8.0 9.7 10.0或-2
8.0 9.7 10.0或-2
11. 12.
12.
二、13.C 14.B 15.D 16.A
三、17.解:(1) ;
;
(2) ;
;
(3)表面积S=48.
18.解:(1)  ,
,

(2)
由 ,得当
,得当 时,
时, 取得最小值-2
取得最小值-2
19.解:(1)

(2)
 ,①
,①
 ,②
,②
②-①,整理,得
20.解:(1) ,设
,设
则
任取 ,
, ,
,
当 时,
时, 单调递减;
单调递减;
当 时,
时, 单调递增.
单调递增.
由 得
得
 的值域为
的值域为 .
.
(2)设 ,
,
则 ,
,
所以 单调递减.
单调递减.
(3)由 的值域为:
的值域为:
所以满足题设仅需:
解得, .
.
21.解:(1)
又
(2) 应用第(1)小题结论,得
应用第(1)小题结论,得 取倒数,得
取倒数,得
(3)由正弦定理,原题⇔△ABC中,求证:
证明:由(2)的结论得, 且
且 均小于1,
均小于1,
 ,
,

(4)如得出:四边形ABCD中,求证: 且证明正确给3分;
且证明正确给3分;
如得出:凸n边形A 求证:
求证:
 且证明正确给4分.
且证明正确给4分.
如能应用到其它内容有创意则给高分.
如得出: 为各项为正数的等差数列,
为各项为正数的等差数列, ,求证:
,求证:
 .
.
已知:函数f(x)=ax+
+c(a、b、c是常数)是奇函数,且满足f(1)=
,f(2)=
,
(Ⅰ)求a、b、c的值;
(Ⅱ)试判断函数f(x)在区间(0,
)上的单调性并证明.
查看习题详情和答案>>
| b |
| x |
| 5 |
| 2 |
| 17 |
| 4 |
(Ⅰ)求a、b、c的值;
(Ⅱ)试判断函数f(x)在区间(0,
| 1 |
| 2 |
已知:函数f(x)=ax+
+c(a,b,c是常数)是奇函数,且满足f(1)=
,f(2)=
(1)求a,b,c的值;
(2)试判断函数f(x)在区间(0,
)上的单调性并说明理由;
(3)试求函数f(x)在区间(0,+∞)上的最小值.
查看习题详情和答案>>
| b |
| x |
| 5 |
| 2 |
| 17 |
| 4 |
(1)求a,b,c的值;
(2)试判断函数f(x)在区间(0,
| 1 |
| 2 |
(3)试求函数f(x)在区间(0,+∞)上的最小值.
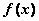 是
是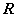 上的奇函数,且满足
上的奇函数,且满足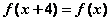 ,当
,当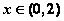 时,
时,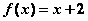 ,则
,则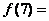 (
)
(
)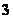 B.
B.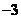 C.
C.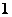 D.
D.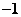
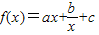 (a、b、c是常数)是奇函数,且满足
(a、b、c是常数)是奇函数,且满足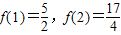 ,
,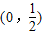 上的单调性并证明.
上的单调性并证明.